Question Number 161442 by nadovic last updated on 18/Dec/21

$$\mathrm{Use}\:\mathrm{the}\:\mathrm{binomial}\:\mathrm{theorem}\:\mathrm{to}\:\mathrm{write} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expansion} \\ $$$$\mathrm{of}\:\sqrt{\mathrm{2}+\mathrm{3}{x}−{x}^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 18/Dec/21
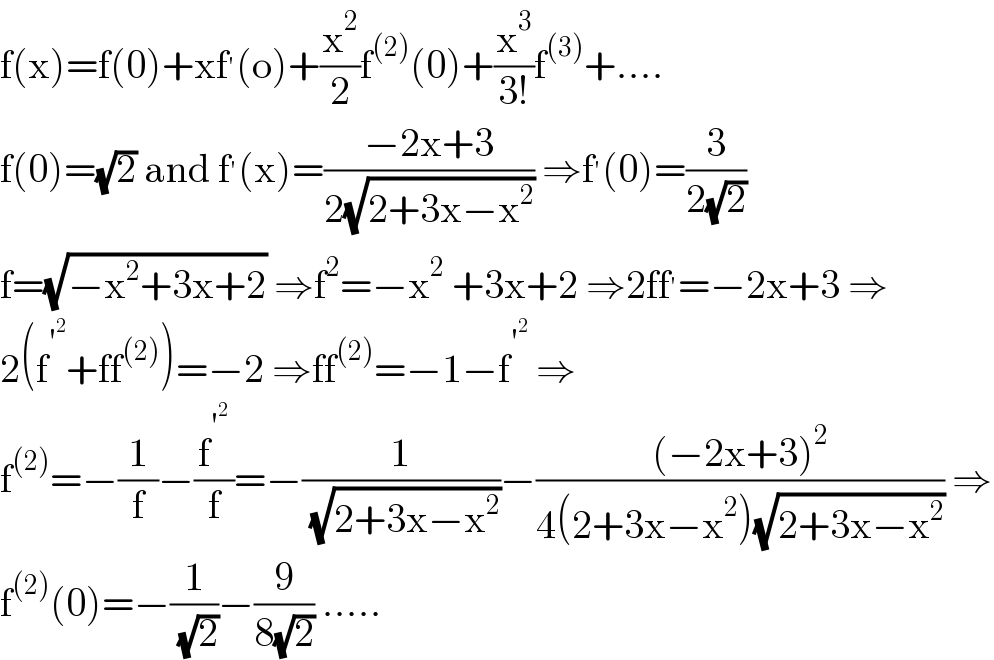
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{0}\right)+\mathrm{xf}^{'} \left(\mathrm{o}\right)+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\mathrm{f}^{\left(\mathrm{3}\right)} +…. \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{−\mathrm{2x}+\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}+\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)=\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{f}=\sqrt{−\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}}\:\Rightarrow\mathrm{f}^{\mathrm{2}} =−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{2}\:\Rightarrow\mathrm{2ff}^{'} =−\mathrm{2x}+\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{2}\left(\mathrm{f}^{'^{\mathrm{2}} } +\mathrm{ff}^{\left(\mathrm{2}\right)} \right)=−\mathrm{2}\:\Rightarrow\mathrm{ff}^{\left(\mathrm{2}\right)} =−\mathrm{1}−\mathrm{f}^{'^{\mathrm{2}} } \:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} =−\frac{\mathrm{1}}{\mathrm{f}}−\frac{\mathrm{f}^{'^{\mathrm{2}} } }{\mathrm{f}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}+\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }}−\frac{\left(−\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{2}+\mathrm{3x}−\mathrm{x}^{\mathrm{2}} \right)\sqrt{\mathrm{2}+\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{9}}{\mathrm{8}\sqrt{\mathrm{2}}}\:….. \\ $$
Commented by nadovic last updated on 18/Dec/21

$${Thank}\:{you}\:{Sir} \\ $$
