Question Number 65781 by gunawan last updated on 03/Aug/19
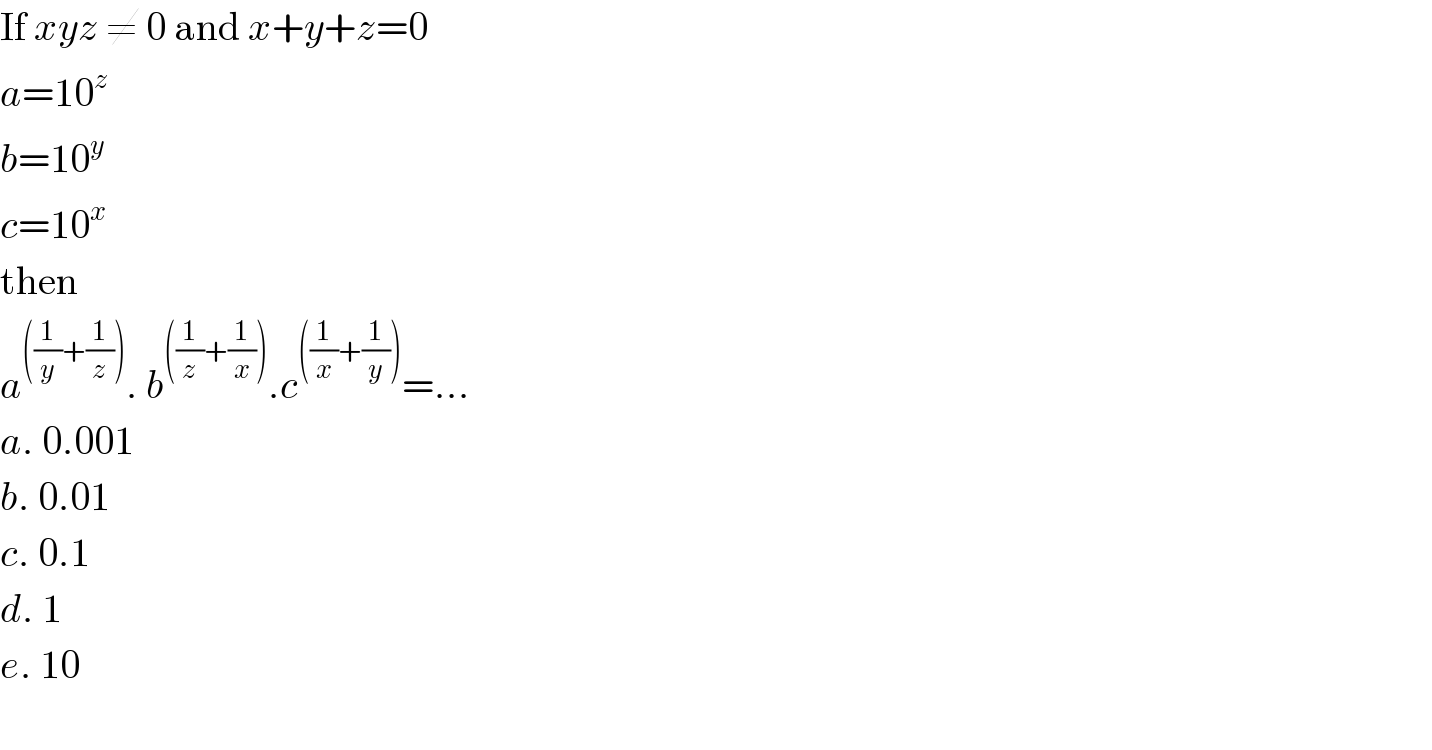
$$\mathrm{If}\:{xyz}\:\neq\:\mathrm{0}\:\mathrm{and}\:{x}+{y}+{z}=\mathrm{0} \\ $$$${a}=\mathrm{10}^{{z}} \\ $$$${b}=\mathrm{10}^{{y}} \\ $$$${c}=\mathrm{10}^{{x}} \\ $$$$\mathrm{then} \\ $$$${a}^{\left(\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)} .\:{b}^{\left(\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}\right)} .{c}^{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)} =… \\ $$$${a}.\:\mathrm{0}.\mathrm{001} \\ $$$${b}.\:\mathrm{0}.\mathrm{01} \\ $$$${c}.\:\mathrm{0}.\mathrm{1} \\ $$$${d}.\:\mathrm{1} \\ $$$${e}.\:\mathrm{10} \\ $$$$ \\ $$
Answered by Tanmay chaudhury last updated on 03/Aug/19
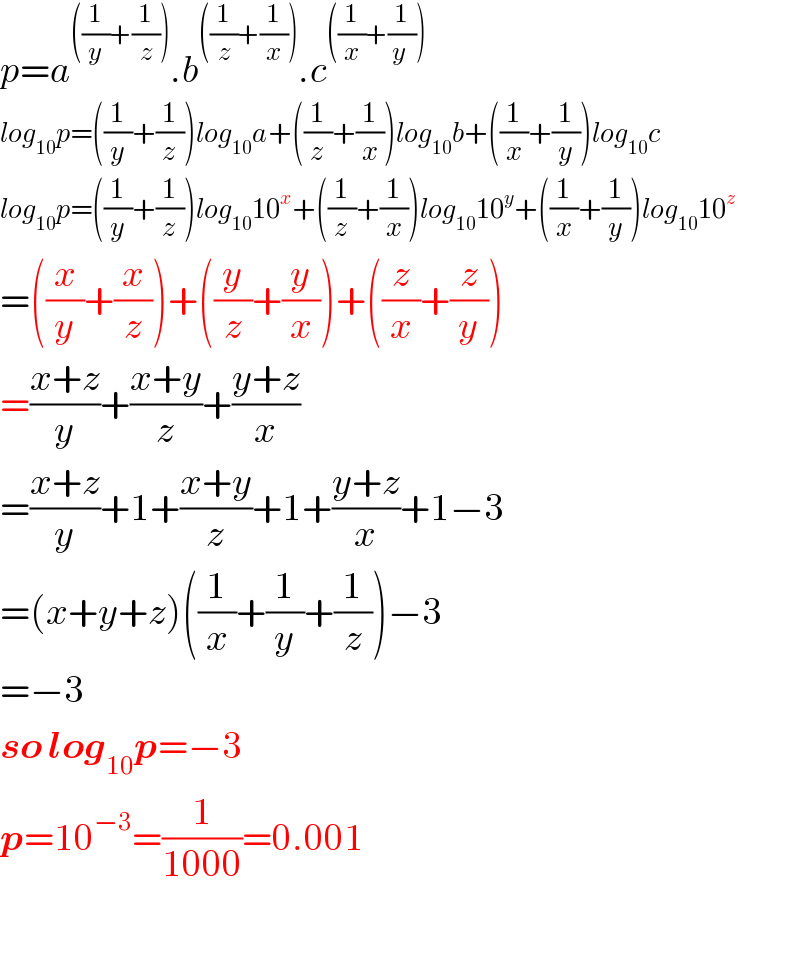
$${p}={a}^{\left(\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)} .{b}^{\left(\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}\right)} .{c}^{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}\:}\right)} \\ $$$${log}_{\mathrm{10}} {p}=\left(\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right){log}_{\mathrm{10}} {a}+\left(\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}\right){log}_{\mathrm{10}} {b}+\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right){log}_{\mathrm{10}} {c} \\ $$$${log}_{\mathrm{10}} {p}=\left(\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right){log}_{\mathrm{10}} \mathrm{10}^{{x}} +\left(\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}\right){log}_{\mathrm{10}} \mathrm{10}^{{y}} +\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right){log}_{\mathrm{10}} \mathrm{10}^{{z}} \\ $$$$=\left(\frac{{x}}{{y}}+\frac{{x}}{{z}}\right)+\left(\frac{{y}}{{z}}+\frac{{y}}{{x}}\right)+\left(\frac{{z}}{{x}}+\frac{{z}}{{y}}\right) \\ $$$$=\frac{{x}+{z}}{{y}}+\frac{{x}+{y}}{{z}}+\frac{{y}+{z}}{{x}} \\ $$$$=\frac{{x}+{z}}{{y}}+\mathrm{1}+\frac{{x}+{y}}{{z}}+\mathrm{1}+\frac{{y}+{z}}{{x}}+\mathrm{1}−\mathrm{3} \\ $$$$=\left({x}+{y}+{z}\right)\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)−\mathrm{3} \\ $$$$=−\mathrm{3} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{log}}_{\mathrm{10}} \boldsymbol{{p}}=−\mathrm{3} \\ $$$$\boldsymbol{{p}}=\mathrm{10}^{−\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1000}}=\mathrm{0}.\mathrm{001} \\ $$$$ \\ $$
Commented by gunawan last updated on 03/Aug/19

$$\mathrm{wow} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by Tanmay chaudhury last updated on 04/Aug/19

$${most}\:{welcome}… \\ $$
