let-give-s-x-n-1-nx-n-and-w-x-n-1-1-n-x-n-1-for-x-lt-1-find-s-x-w-x-at-form-of-series-2-find-s-x-w-x-at-form-of-function-

Tinku Tara June 4, 2023 Relation and Functions 0 Comments

Question Number 30407 by abdo imad last updated on 22/Feb/18

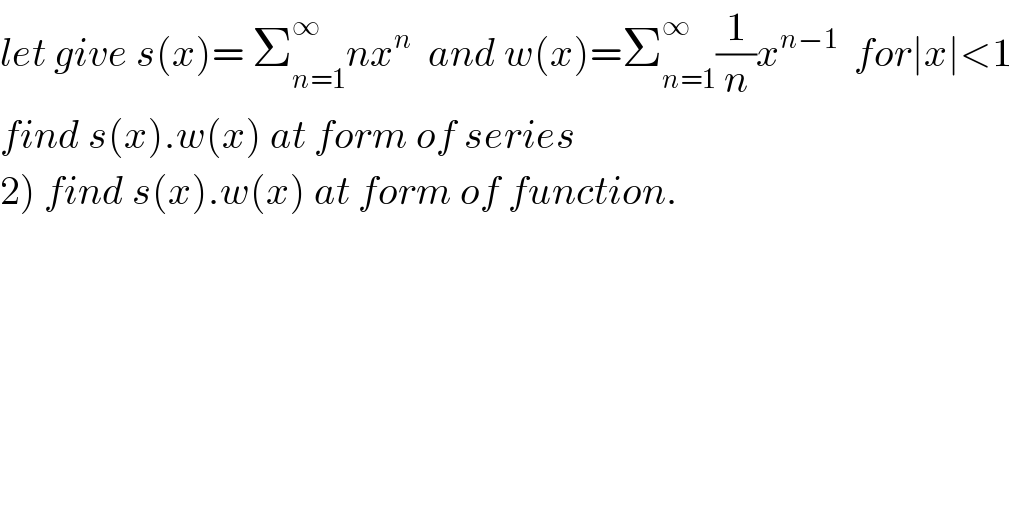
let give s(x)= Σ_(n=1) ^∞ nx^n and w(x)=Σ_(n=1) ^∞ (1/n)x^(n−1) for∣x∣<1 find s(x).w(x) at form of series 2) find s(x).w(x) at form of function.

$${let}\:{give}\:{s}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} {nx}^{{n}} \:\:{and}\:{w}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}{x}^{{n}−\mathrm{1}} \:\:{for}\mid{x}\mid<\mathrm{1} \\ $$$${find}\:{s}\left({x}\right).{w}\left({x}\right)\:{at}\:{form}\:{of}\:{series} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{s}\left({x}\right).{w}\left({x}\right)\:{at}\:{form}\:{of}\:{function}. \\ $$

Facebook Tweet Pin

let-give-s-x-n-1-nx-n-and-w-x-n-1-1-n-x-n-1-for-x-lt-1-find-s-x-w-x-at-form-of-series-2-find-s-x-w-x-at-form-of-function-

Leave a Reply Cancel reply