Question-161482

Facebook Tweet Pin

Question Number 161482 by amin96 last updated on 18/Dec/21

Commented by amin96 last updated on 18/Dec/21

$${circles}\:{area}=? \\ $$

Answered by FongXD last updated on 18/Dec/21

Commented by Tawa11 last updated on 18/Dec/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Answered by FongXD last updated on 18/Dec/21

Commented by amin96 last updated on 18/Dec/21

$${great}\:{sir}\:{weldone} \\ $$

Commented by mr W last updated on 18/Dec/21

$${nice}\:{job}! \\ $$

Answered by mr W last updated on 18/Dec/21

Commented by mr W last updated on 18/Dec/21

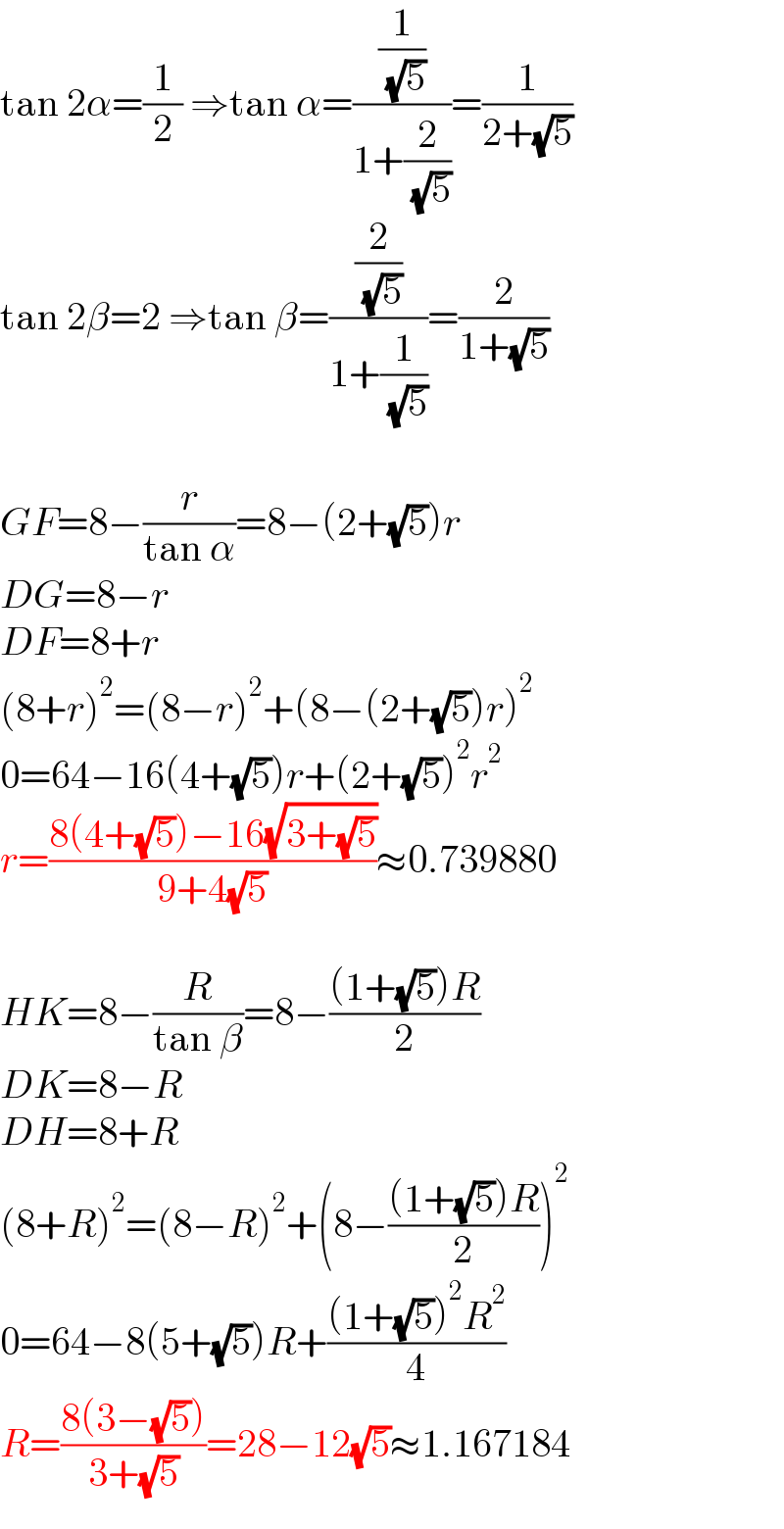
tan 2α=(1/2) ⇒tan α=((1/( (√5)))/(1+(2/( (√5)))))=(1/(2+(√5))) tan 2β=2 ⇒tan β=((2/( (√5)))/(1+(1/( (√5)))))=(2/(1+(√5))) GF=8−(r/(tan α))=8−(2+(√5))r DG=8−r DF=8+r (8+r)^2 =(8−r)^2 +(8−(2+(√5))r)^2 0=64−16(4+(√5))r+(2+(√5))^2 r^2 r=((8(4+(√5))−16(√(3+(√5))))/(9+4(√5)))≈0.739880 HK=8−(R/(tan β))=8−(((1+(√5))R)/2) DK=8−R DH=8+R (8+R)^2 =(8−R)^2 +(8−(((1+(√5))R)/2))^2 0=64−8(5+(√5))R+(((1+(√5))^2 R^2 )/4) R=((8(3−(√5)))/(3+(√5)))=28−12(√5)≈1.167184

$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{5}}} \\ $$$$\mathrm{tan}\:\mathrm{2}\beta=\mathrm{2}\:\Rightarrow\mathrm{tan}\:\beta=\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}}=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{5}}} \\ $$$$ \\ $$$${GF}=\mathrm{8}−\frac{{r}}{\mathrm{tan}\:\alpha}=\mathrm{8}−\left(\mathrm{2}+\sqrt{\mathrm{5}}\right){r} \\ $$$${DG}=\mathrm{8}−{r} \\ $$$${DF}=\mathrm{8}+{r} \\ $$$$\left(\mathrm{8}+{r}\right)^{\mathrm{2}} =\left(\mathrm{8}−{r}\right)^{\mathrm{2}} +\left(\mathrm{8}−\left(\mathrm{2}+\sqrt{\mathrm{5}}\right){r}\right)^{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{64}−\mathrm{16}\left(\mathrm{4}+\sqrt{\mathrm{5}}\right){r}+\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$${r}=\frac{\mathrm{8}\left(\mathrm{4}+\sqrt{\mathrm{5}}\right)−\mathrm{16}\sqrt{\mathrm{3}+\sqrt{\mathrm{5}}}}{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}}\approx\mathrm{0}.\mathrm{739880} \\ $$$$ \\ $$$${HK}=\mathrm{8}−\frac{{R}}{\mathrm{tan}\:\beta}=\mathrm{8}−\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){R}}{\mathrm{2}} \\ $$$${DK}=\mathrm{8}−{R} \\ $$$${DH}=\mathrm{8}+{R} \\ $$$$\left(\mathrm{8}+{R}\right)^{\mathrm{2}} =\left(\mathrm{8}−{R}\right)^{\mathrm{2}} +\left(\mathrm{8}−\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){R}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{64}−\mathrm{8}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right){R}+\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} {R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${R}=\frac{\mathrm{8}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)}{\mathrm{3}+\sqrt{\mathrm{5}}}=\mathrm{28}−\mathrm{12}\sqrt{\mathrm{5}}\approx\mathrm{1}.\mathrm{167184} \\ $$

Commented by Ar Brandon last updated on 19/Dec/21

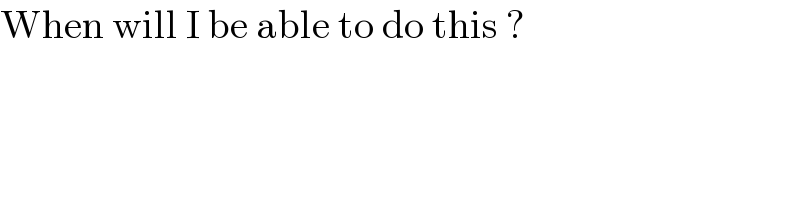
$$\mathrm{When}\:\mathrm{will}\:\mathrm{I}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{do}\:\mathrm{this}\:? \\ $$

Commented by mr W last updated on 19/Dec/21

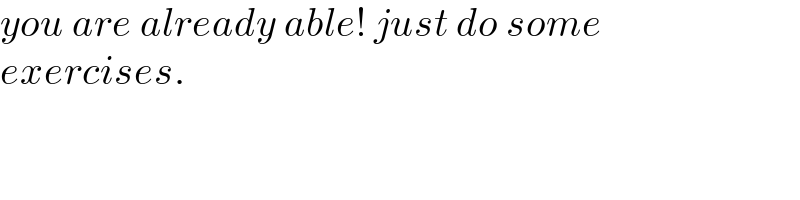
$${you}\:{are}\:{already}\:{able}!\:{just}\:{do}\:{some} \\ $$$${exercises}. \\ $$

Commented by peter frank last updated on 19/Dec/21

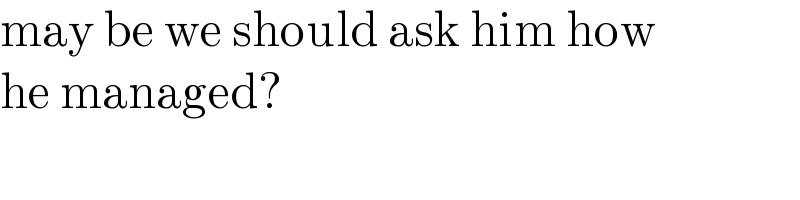
may be we should ask him how he managed?

$$\mathrm{may}\:\mathrm{be}\:\mathrm{we}\:\mathrm{should}\:\mathrm{ask}\:\mathrm{him}\:\mathrm{how} \\ $$$$\mathrm{he}\:\mathrm{managed}? \\ $$

Commented by peter frank last updated on 19/Dec/21

To mrW.we thank you very much for being here in this forum we learn alot from you(Physics,Maths)

$$\mathrm{To}\:\mathrm{mrW}.\mathrm{we}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$$$\mathrm{for}\:\mathrm{being}\:\mathrm{here}\:\mathrm{in}\:\mathrm{this}\:\mathrm{forum} \\ $$$$\mathrm{we}\:\mathrm{learn}\:\mathrm{alot}\:\mathrm{from}\:\mathrm{you}\left(\mathrm{Physics},\mathrm{Maths}\right) \\ $$

Commented by mr W last updated on 19/Dec/21

$${thanks}\:{for}\:{feedback}!\:{if}\:{i}\:{could}\:{help}\: \\ $$$${you}\:{somehow},\:{i}\:{did}\:{with}\:{pleasure}. \\ $$

Commented by Ar Brandon last updated on 19/Dec/21

Alright Sir. But I need some ressources. I have none. Documents on this topic.

$$\mathrm{Alright}\:\mathrm{Sir}.\:\mathrm{But}\:\mathrm{I}\:\mathrm{need}\:\mathrm{some}\:\mathrm{ressources}. \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{none}.\:\mathrm{Documents}\:\mathrm{on}\:\mathrm{this}\:\mathrm{topic}. \\ $$

Commented by mr W last updated on 20/Dec/21

$${try}\:{to}\:{find}\:{the}\:{radii}\:{of}\:{the}\:{three}\:{new} \\ $$$${circles}\:{if}\:{you}\:{want}: \\ $$

Commented by mr W last updated on 20/Dec/21

Commented by Ar Brandon last updated on 20/Dec/21

Sir, I notice the smallest radius is (R/2) But have no idea on how to solve the others.

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{notice}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{radius}\:\mathrm{is}\:\frac{\mathrm{R}}{\mathrm{2}} \\ $$$$\mathrm{But}\:\mathrm{have}\:\mathrm{no}\:\mathrm{idea}\:\mathrm{on}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{others}. \\ $$

Commented by Ar Brandon last updated on 20/Dec/21

Commented by Ar Brandon last updated on 20/Dec/21

Here is my sketch. I don′t know what to do next.

$$\mathrm{Here}\:\mathrm{is}\:\mathrm{my}\:\mathrm{sketch}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{what}\:\mathrm{to}\:\mathrm{do}\:\mathrm{next}. \\ $$

Commented by mr W last updated on 20/Dec/21