Question Number 30436 by abdo imad last updated on 22/Feb/18
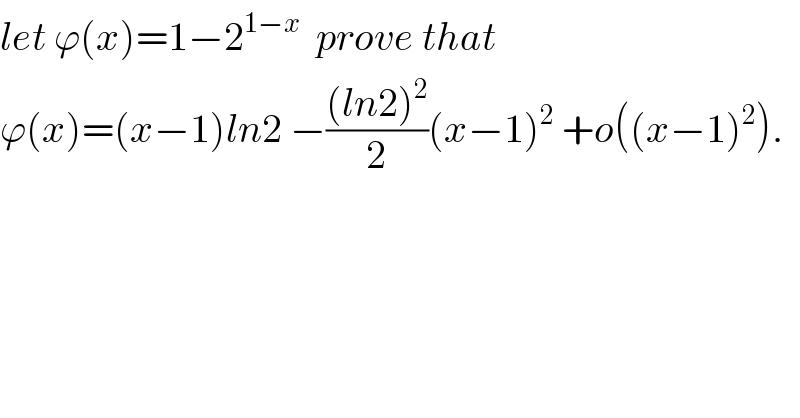
$${let}\:\varphi\left({x}\right)=\mathrm{1}−\mathrm{2}^{\mathrm{1}−{x}} \:\:{prove}\:{that} \\ $$$$\varphi\left({x}\right)=\left({x}−\mathrm{1}\right){ln}\mathrm{2}\:−\frac{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+{o}\left(\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right). \\ $$
Commented by prof Abdo imad last updated on 22/Feb/18

$${x}\rightarrow\mathrm{1} \\ $$
Answered by sma3l2996 last updated on 24/Feb/18
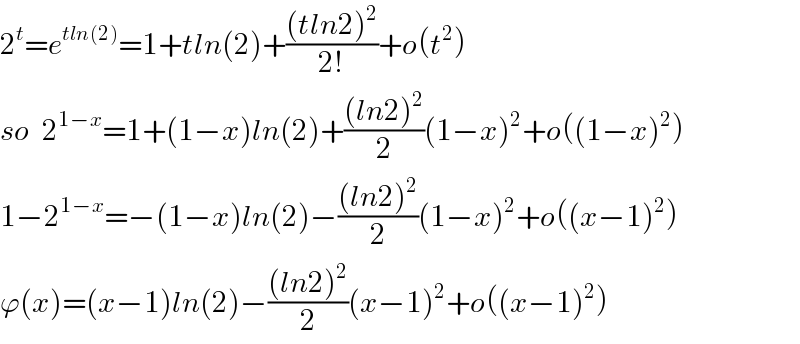
$$\mathrm{2}^{{t}} ={e}^{{tln}\left(\mathrm{2}\right)} =\mathrm{1}+{tln}\left(\mathrm{2}\right)+\frac{\left({tln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}!}+{o}\left({t}^{\mathrm{2}} \right) \\ $$$${so}\:\:\mathrm{2}^{\mathrm{1}−{x}} =\mathrm{1}+\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{2}\right)+\frac{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +{o}\left(\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \right) \\ $$$$\mathrm{1}−\mathrm{2}^{\mathrm{1}−{x}} =−\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{2}\right)−\frac{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +{o}\left(\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right) \\ $$$$\varphi\left({x}\right)=\left({x}−\mathrm{1}\right){ln}\left(\mathrm{2}\right)−\frac{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{o}\left(\left({x}−\mathrm{1}\right)^{\mathrm{2}} \right) \\ $$
