Question Number 161521 by vvvv last updated on 19/Dec/21
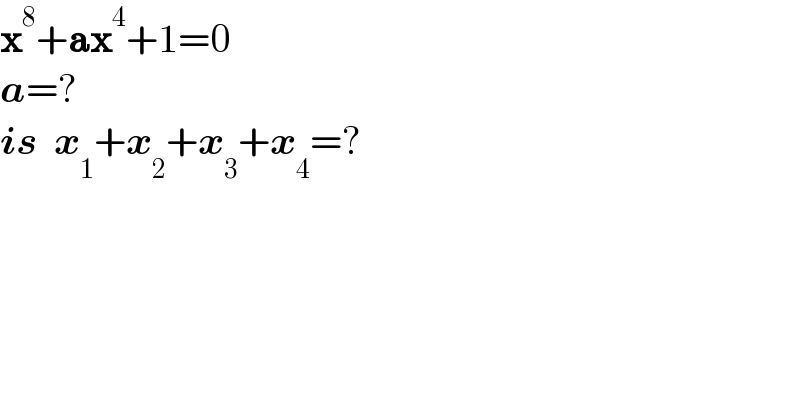
$$\boldsymbol{\mathrm{x}}^{\mathrm{8}} +\boldsymbol{\mathrm{ax}}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$$\boldsymbol{{a}}=?\: \\ $$$$\boldsymbol{{is}}\:\:\boldsymbol{{x}}_{\mathrm{1}} +\boldsymbol{{x}}_{\mathrm{2}} +\boldsymbol{{x}}_{\mathrm{3}} +\boldsymbol{{x}}_{\mathrm{4}} =? \\ $$
Commented by mr W last updated on 19/Dec/21

$${though}\:{you}\:{used}\:{two}\:{times}\:{the}\:{question} \\ $$$${mark},\:{but}\:{you}\:{didn}'{t}\:{put}\:{a}\:{clear}\: \\ $$$${question}.\:{what}\:{is}\:{your}\:{exact}\:{question}? \\ $$
Commented by Tyller last updated on 19/Dec/21
![(x^4 )^2 +ax^4 +1=0 (x^4 +(a/2))^2 =((a^2 −4)/4) x=±((−(a/2)±(√((a^2 −4)/4)).))^(1/4) a∈[0,(√2)] x_1 +x_2 +x_3 +x_4 =0](https://www.tinkutara.com/question/Q161531.png)
$$\left({x}^{\mathrm{4}} \right)^{\mathrm{2}} +{ax}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} +\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}} \\ $$$${x}=\pm\sqrt[{\mathrm{4}}]{−\frac{{a}}{\mathrm{2}}\pm\sqrt{\frac{{a}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}}}.} \\ $$$${a}\in\left[\mathrm{0},\sqrt{\mathrm{2}}\right] \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} =\mathrm{0} \\ $$
Commented by mr W last updated on 19/Dec/21

$${it}\:{is}\:{not}\:{stated}\:{that}\:{x}\in\mathbb{R}.\:{so}\:{a}\:{can}\:{be} \\ $$$${any}\:{value}\:{and}\:{there}\:{are}\:{generally}\:\mathrm{8} \\ $$$${roots}. \\ $$$${that}\:{is}\:{why}\:{i}\:{said}\:{the}\:{question}\:{is}\:{not} \\ $$$${clear}. \\ $$
