Question Number 161564 by HongKing last updated on 19/Dec/21
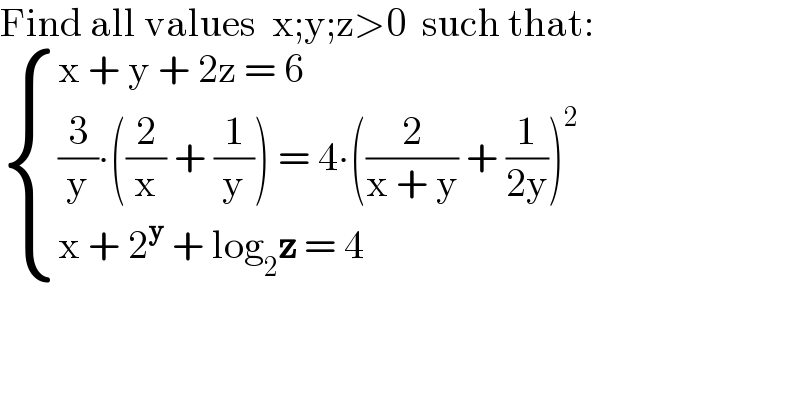
$$\mathrm{Find}\:\mathrm{all}\:\mathrm{values}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\begin{cases}{\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{2z}\:=\:\mathrm{6}}\\{\frac{\mathrm{3}}{\mathrm{y}}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\right)\:=\:\mathrm{4}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}\:+\:\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{2y}}\right)^{\mathrm{2}} }\\{\mathrm{x}\:+\:\mathrm{2}^{\boldsymbol{\mathrm{y}}} \:+\:\mathrm{log}_{\mathrm{2}} \boldsymbol{\mathrm{z}}\:=\:\mathrm{4}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Dec/21

$$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{2}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 20/Dec/21
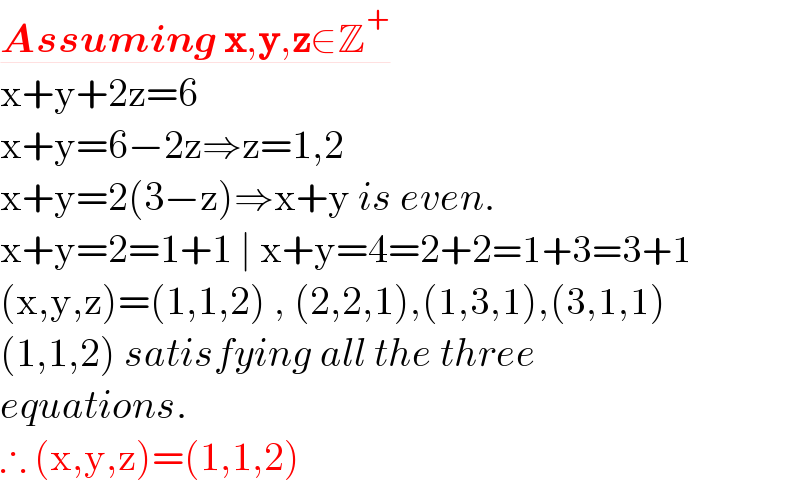
$$\underline{\boldsymbol{{Assuming}}\:\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}\in\mathbb{Z}^{+} } \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{2z}=\mathrm{6} \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{6}−\mathrm{2z}\Rightarrow\mathrm{z}=\mathrm{1},\mathrm{2} \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{2}\left(\mathrm{3}−\mathrm{z}\right)\Rightarrow\mathrm{x}+\mathrm{y}\:{is}\:{even}. \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{2}=\mathrm{1}+\mathrm{1}\:\mid\:\mathrm{x}+\mathrm{y}=\mathrm{4}=\mathrm{2}+\mathrm{2}=\mathrm{1}+\mathrm{3}=\mathrm{3}+\mathrm{1} \\ $$$$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{2}\right)\:,\:\left(\mathrm{2},\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},\mathrm{3},\mathrm{1}\right),\left(\mathrm{3},\mathrm{1},\mathrm{1}\right) \\ $$$$\left(\mathrm{1},\mathrm{1},\mathrm{2}\right)\:{satisfying}\:{all}\:{the}\:{three} \\ $$$${equations}. \\ $$$$\therefore\:\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{2}\right) \\ $$
Commented by HongKing last updated on 20/Dec/21
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
