Question Number 161586 by blackmamba last updated on 20/Dec/21

$$\:\:\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{2cos}\:\sqrt{{x}−\mathrm{2}}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:=? \\ $$
Commented by cortano last updated on 20/Dec/21

Commented by mathmax by abdo last updated on 20/Dec/21

$$\mathrm{sir}\:\mathrm{cortano}\:\mathrm{you}\:\mathrm{take}\:\mathrm{another}\:\mathrm{limit}\:\mathrm{loook}\:\mathrm{the}\:\mathrm{Q}… \\ $$
Answered by TheSupreme last updated on 20/Dec/21

$${t}={x}−\mathrm{2} \\ $$$${lim}\:\frac{\mathrm{2}−\mathrm{2}{cos}\left(\sqrt{{t}}\right)}{{t}^{\mathrm{2}} }=\mathrm{2}\frac{\mathrm{1}−{cos}\left(\sqrt{{t}}\right)}{{t}^{\mathrm{2}} }=\mathrm{2}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} }=\infty \\ $$
Commented by cortano last updated on 20/Dec/21

$${the}\:{question} \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\frac{{x}−\mathrm{2cos}\:\sqrt{\mathrm{2}−{x}}}{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} } \\ $$$$\:\sqrt{\mathrm{2}−{x}}\:{defined}\:{on}\:\mathrm{2}−{x}\geqslant\mathrm{0} \\ $$$$\:\Rightarrow{x}\leqslant\mathrm{2}\: \\ $$
Commented by cortano last updated on 20/Dec/21

$${why}\:{not}\:{valid}? \\ $$
Commented by cortano last updated on 20/Dec/21

$${Answer}\:−\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Commented by mr W last updated on 20/Dec/21

$$−\frac{\mathrm{1}}{\mathrm{12}}\:{is}\:{wrong}. \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\:\left(…\right)=+\infty \\ $$$${x}<\mathrm{2}\:{is}\:{not}\:{valid}. \\ $$
Commented by mnjuly1970 last updated on 20/Dec/21
![D_( f) = (∞ ,2]](https://www.tinkutara.com/question/Q161610.png)
$$\:\:\:\mathrm{D}_{\:{f}} \:\:=\:\left(\infty\:,\mathrm{2}\right] \\ $$
Commented by mr W last updated on 20/Dec/21
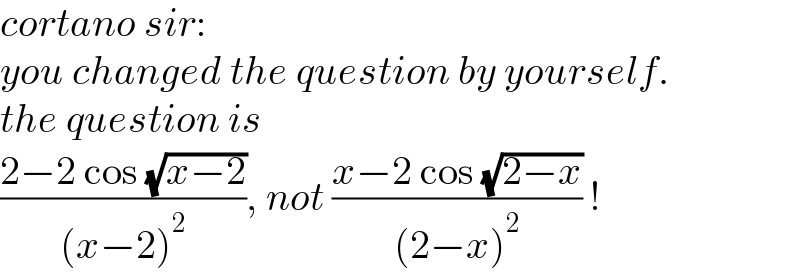
$${cortano}\:{sir}: \\ $$$${you}\:{changed}\:{the}\:{question}\:{by}\:{yourself}. \\ $$$${the}\:{question}\:{is} \\ $$$$\frac{\mathrm{2}−\mathrm{2}\:\mathrm{cos}\:\sqrt{{x}−\mathrm{2}}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} },\:{not}\:\frac{{x}−\mathrm{2}\:\mathrm{cos}\:\sqrt{\mathrm{2}−{x}}}{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }\:! \\ $$
Answered by mathmax by abdo last updated on 20/Dec/21

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}−\mathrm{2cos}\sqrt{\mathrm{x}−\mathrm{2}}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{x}−\mathrm{2}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}−\mathrm{2cost}}{\mathrm{t}^{\mathrm{4}} }\:\:\:\:\:\:\left(\mathrm{x}\rightarrow\mathrm{2}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\mathrm{cost}\sim\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{2}−\mathrm{2}+\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:\rightarrow+\infty \\ $$
