Question Number 30518 by abdo imad last updated on 22/Feb/18
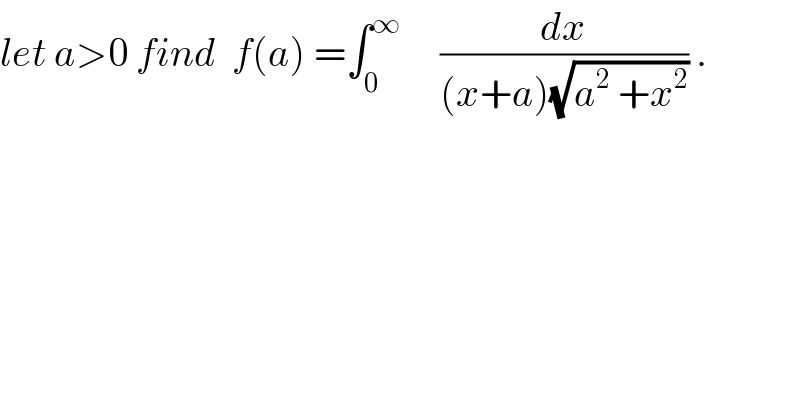
$${let}\:{a}>\mathrm{0}\:{find}\:\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}+{a}\right)\sqrt{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }}\:. \\ $$
Answered by sma3l2996 last updated on 24/Feb/18
![f(a)=∫_0 ^∞ (dx/(a^2 ((x/a)+1)(√(((x/a))^2 +1)))) let (x/a)=sinh(t)⇒dx=a×cosh(t)dt=a(√(1+sinh^2 t))dt dt=(dx/(a(√(1+((x/a))^2 )))) f(a)=(1/a)∫_0 ^∞ (dt/((sinh(t)+1)))=(1/a)∫_0 ^∞ (e^t /(e^(2t) +e^t −1))dt =(1/a)∫_0 ^∞ (e^t /((((2e^t +1)/2))^2 −(5/4)))dt=(1/a)∫_0 ^∞ (e^t /((5/4)((((2e^t +1)/( (√5))))^2 −1)))dt u=((2e^t +1)/( (√5)))⇒du=(2/( (√5)))e^t dt e^t dt=((√5)/2)du f(a)=((2(√5))/(5a))∫_(1/(√5)) ^∞ (du/(u^2 −1))=((2(√5))/(5a))∫_(1/(√5)) ^∞ (du/((u+1)(u−1))) f(a)=((√5)/(5a))[ln∣((u−1)/(u+1))∣]_(1/(√5)) ^∞ =−((√5)/(5a))ln∣((1/(√5)−1)/(1/(√5)+1))∣ =((√5)/(5a))ln∣((1+(√5))/(1−(√5)))∣=((2(√5))/(5a))ln(((1+(√5))/2))](https://www.tinkutara.com/question/Q30695.png)
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}^{\mathrm{2}} \left(\frac{{x}}{{a}}+\mathrm{1}\right)\sqrt{\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\mathrm{1}}} \\ $$$${let}\:\:\frac{{x}}{{a}}={sinh}\left({t}\right)\Rightarrow{dx}={a}×{cosh}\left({t}\right){dt}={a}\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {t}}{dt} \\ $$$${dt}=\frac{{dx}}{{a}\sqrt{\mathrm{1}+\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} }} \\ $$$${f}\left({a}\right)=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left({sinh}\left({t}\right)+\mathrm{1}\right)}=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{t}} }{{e}^{\mathrm{2}{t}} +{e}^{{t}} −\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{t}} }{\left(\frac{\mathrm{2}{e}^{{t}} +\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}}{dt}=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{t}} }{\frac{\mathrm{5}}{\mathrm{4}}\left(\left(\frac{\mathrm{2}{e}^{{t}} +\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$${u}=\frac{\mathrm{2}{e}^{{t}} +\mathrm{1}}{\:\sqrt{\mathrm{5}}}\Rightarrow{du}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}{e}^{{t}} {dt} \\ $$$${e}^{{t}} {dt}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{du} \\ $$$${f}\left({a}\right)=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}{a}}\int_{\mathrm{1}/\sqrt{\mathrm{5}}} ^{\infty} \frac{{du}}{{u}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}{a}}\int_{\mathrm{1}/\sqrt{\mathrm{5}}} ^{\infty} \frac{{du}}{\left({u}+\mathrm{1}\right)\left({u}−\mathrm{1}\right)} \\ $$$${f}\left({a}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}{a}}\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\mathrm{1}/\sqrt{\mathrm{5}}} ^{\infty} =−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}{a}}{ln}\mid\frac{\mathrm{1}/\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{1}/\sqrt{\mathrm{5}}+\mathrm{1}}\mid \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}{a}}{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{1}−\sqrt{\mathrm{5}}}\mid=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}{a}}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$ \\ $$
