Question Number 96076 by bobhans last updated on 29/May/20
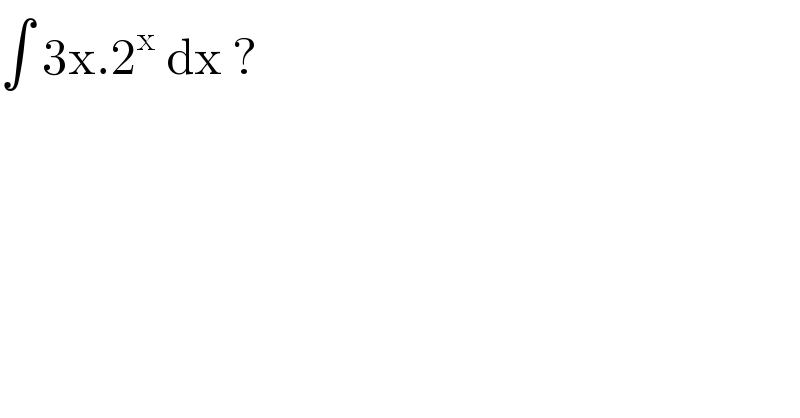
$$\int\:\mathrm{3x}.\mathrm{2}^{\mathrm{x}} \:\mathrm{dx}\:?\: \\ $$
Answered by i jagooll last updated on 29/May/20
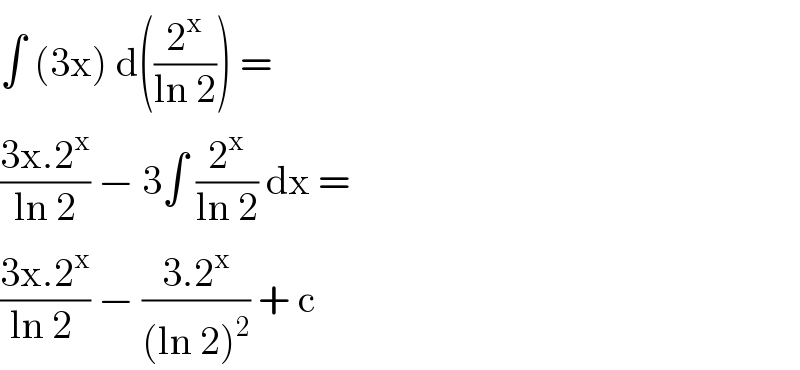
$$\int\:\left(\mathrm{3x}\right)\:\mathrm{d}\left(\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{ln}\:\mathrm{2}}\right)\:=\: \\ $$$$\frac{\mathrm{3x}.\mathrm{2}^{\mathrm{x}} }{\mathrm{ln}\:\mathrm{2}}\:−\:\mathrm{3}\int\:\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{ln}\:\mathrm{2}}\:\mathrm{dx}\:=\: \\ $$$$\frac{\mathrm{3x}.\mathrm{2}^{\mathrm{x}} }{\mathrm{ln}\:\mathrm{2}\:}\:−\:\frac{\mathrm{3}.\mathrm{2}^{\mathrm{x}} }{\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} }\:+\:\mathrm{c}\: \\ $$
Answered by abdomathmax last updated on 29/May/20
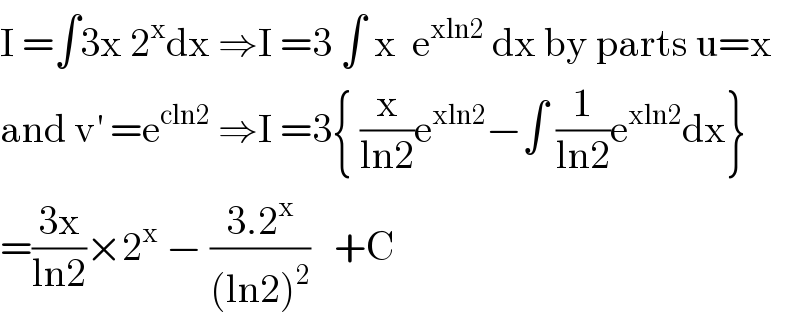
$$\mathrm{I}\:=\int\mathrm{3x}\:\mathrm{2}^{\mathrm{x}} \mathrm{dx}\:\Rightarrow\mathrm{I}\:=\mathrm{3}\:\int\:\mathrm{x}\:\:\mathrm{e}^{\mathrm{xln2}} \:\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}=\mathrm{x} \\ $$$$\mathrm{and}\:\mathrm{v}^{'} \:=\mathrm{e}^{\mathrm{cln2}} \:\Rightarrow\mathrm{I}\:=\mathrm{3}\left\{\:\frac{\mathrm{x}}{\mathrm{ln2}}\mathrm{e}^{\mathrm{xln2}} −\int\:\frac{\mathrm{1}}{\mathrm{ln2}}\mathrm{e}^{\mathrm{xln2}} \mathrm{dx}\right\} \\ $$$$=\frac{\mathrm{3x}}{\mathrm{ln2}}×\mathrm{2}^{\mathrm{x}} \:−\:\frac{\mathrm{3}.\mathrm{2}^{\mathrm{x}} }{\left(\mathrm{ln2}\right)^{\mathrm{2}} }\:\:\:+\mathrm{C} \\ $$
