Question Number 30543 by mondodotto@gmail.com last updated on 23/Feb/18
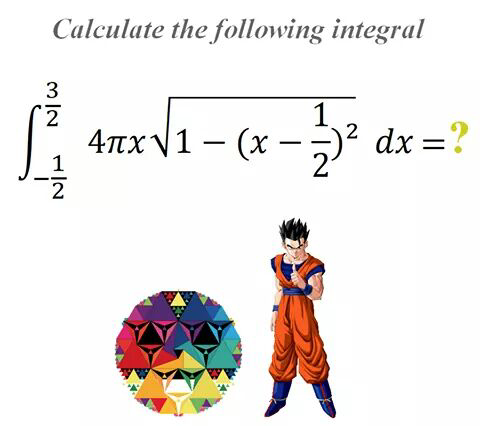
Commented by abdo imad last updated on 23/Feb/18
![the ch.x−(1/2)=sint give I= ∫_(−(π/2)) ^(π/2) 4π((1/2) +sint)(√(1−sin^2 t)) cost dt I= ∫_(−(π/2)) ^(π/2) 4π((1/2) +sint)cos^2 tdt =2π ∫_(−(π/2)) ^(π/2) cos^2 t dt +4π ∫_(−(π/2)) ^(π/2) sint cos^2 t dt but the functiont→sintcos^2 t is odd ⇒∫_(−(π/2)) ^(π/2) sint cos^2 tdt=0 ⇒ I= 4π ∫_0 ^(π/2) (((1+cos(2t))/2))dt I=2π ∫_0 ^(π/2) dt +2π ∫_0 ^(π/2) cos(2t)dt= π^2 +2π[ (1/2)sin(2t)]_0 ^(π/2) = π^2 +0 ⇒ I=π^2 .](https://www.tinkutara.com/question/Q30624.png)
$${the}\:{ch}.{x}−\frac{\mathrm{1}}{\mathrm{2}}={sint}\:{give} \\ $$$${I}=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{4}\pi\left(\frac{\mathrm{1}}{\mathrm{2}}\:+{sint}\right)\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {t}}\:{cost}\:{dt} \\ $$$${I}=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4}\pi\left(\frac{\mathrm{1}}{\mathrm{2}}\:+{sint}\right){cos}^{\mathrm{2}} {tdt}\:=\mathrm{2}\pi\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} {t}\:{dt} \\ $$$$+\mathrm{4}\pi\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{sint}\:{cos}^{\mathrm{2}} {t}\:{dt}\:{but}\:{the}\:{functiont}\rightarrow{sintcos}^{\mathrm{2}} {t}\:{is}\:{odd} \\ $$$$\Rightarrow\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {sint}\:{cos}^{\mathrm{2}} {tdt}=\mathrm{0}\:\Rightarrow\:{I}=\:\mathrm{4}\pi\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$${I}=\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{dt}\:+\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}\left(\mathrm{2}{t}\right){dt}=\:\pi^{\mathrm{2}} \:\:+\mathrm{2}\pi\left[\:\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\pi^{\mathrm{2}} \:+\mathrm{0}\:\Rightarrow\:{I}=\pi^{\mathrm{2}} \:\:. \\ $$
Answered by ajfour last updated on 23/Feb/18
![I= 4π∫_(−1/2) ^( 3/2) (1−x)(√(1−((1/2)−x)^2 )) dx ⇒ 2I =4π∫_(−1/2) ^( 3/2) (√(1−(x−(1/2))^2 )) dx I=2π[(1/2)(x−(1/2))(√(1−(x−(1/2))^2 )) + (1/2)sin^(−1) (x−(1/2))]∣_(−1/2) ^(3/2) I=2π×(1/2)[sin^(−1) 1−sin^(−1) (−1)] ⇒ I = 𝛑^2 .](https://www.tinkutara.com/question/Q30629.png)
$${I}=\:\mathrm{4}\pi\int_{−\mathrm{1}/\mathrm{2}} ^{\:\:\mathrm{3}/\mathrm{2}} \left(\mathrm{1}−{x}\right)\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\Rightarrow\:\mathrm{2}{I}\:=\mathrm{4}\pi\int_{−\mathrm{1}/\mathrm{2}} ^{\:\:\mathrm{3}/\mathrm{2}} \sqrt{\mathrm{1}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$${I}=\mathrm{2}\pi\left[\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{1}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]\mid_{−\mathrm{1}/\mathrm{2}} ^{\mathrm{3}/\mathrm{2}} \\ $$$${I}=\mathrm{2}\pi×\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \mathrm{1}−\mathrm{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right] \\ $$$$\Rightarrow\:\:\:{I}\:=\:\boldsymbol{\pi}^{\mathrm{2}} \:\:. \\ $$
