Question Number 161703 by cortano last updated on 21/Dec/21
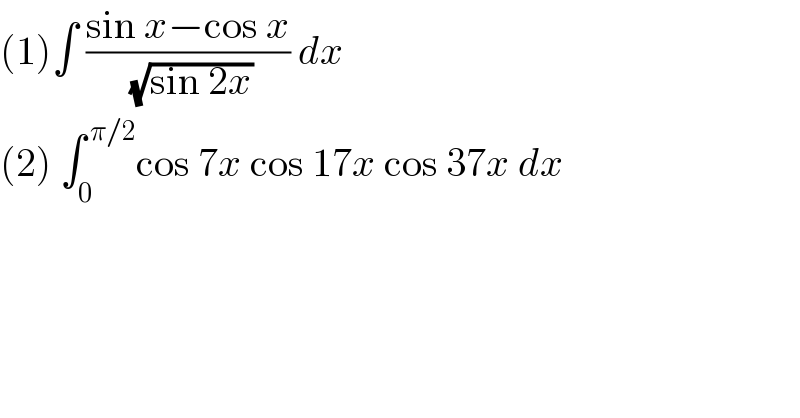
$$\left(\mathrm{1}\right)\int\:\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{sin}\:\mathrm{2}{x}}}\:{dx} \\ $$$$\left(\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{cos}\:\mathrm{7}{x}\:\mathrm{cos}\:\mathrm{17}{x}\:\mathrm{cos}\:\mathrm{37}{x}\:{dx} \\ $$
Commented by cortano last updated on 21/Dec/21
![(1) Ω =∫ ((sin x−cos x)/( (√(1+sin 2x−1)))) dx =∫ ((sin x−cos x)/( (√((sin x+cos x)^2 −1)))) =−∫ ((cos x−sin x)/( (√((sin x+cos x)^2 −1)))) dx [ sin x+cos x= r⇒(cos x−sin x)dx=dr ] Ω =−∫ (dr/( (√(r^2 −1)))) [ r =sec t ⇒dr=sec t tan t dt ] Ω = −∫ ((sec t tan t)/(tan t)) dt Ω =−ln ∣sec t+tan t∣+c Ω=−ln ∣sin x+cos x+(√(sin 2x)) ∣ + c](https://www.tinkutara.com/question/Q161720.png)
$$\left(\mathrm{1}\right)\:\Omega\:=\int\:\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}−\mathrm{1}}}\:{dx} \\ $$$$\:\:\:\:\:\:\:=\int\:\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} −\mathrm{1}}}\: \\ $$$$\:\:\:\:=−\int\:\frac{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{\:\sqrt{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} −\mathrm{1}}}\:{dx} \\ $$$$\:\left[\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}=\:{r}\Rightarrow\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right){dx}={dr}\:\right] \\ $$$$\:\:\Omega\:=−\int\:\frac{{dr}}{\:\sqrt{{r}^{\mathrm{2}} −\mathrm{1}}}\: \\ $$$$\:\left[\:{r}\:=\mathrm{sec}\:{t}\:\Rightarrow{dr}=\mathrm{sec}\:{t}\:\mathrm{tan}\:{t}\:{dt}\:\right] \\ $$$$\:\:\Omega\:=\:−\int\:\frac{\mathrm{sec}\:{t}\:\mathrm{tan}\:{t}}{\mathrm{tan}\:{t}}\:{dt} \\ $$$$\:\:\Omega\:=−\mathrm{ln}\:\mid\mathrm{sec}\:{t}+\mathrm{tan}\:{t}\mid+{c}\: \\ $$$$\:\:\Omega=−\mathrm{ln}\:\mid\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\sqrt{\mathrm{sin}\:\mathrm{2}{x}}\:\mid\:+\:{c} \\ $$
Answered by Ar Brandon last updated on 21/Dec/21

$${I}=\int\frac{\mathrm{sin}{x}−\mathrm{cos}{x}}{\:\sqrt{\mathrm{sin2}{x}}}{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\left(\sqrt{\mathrm{tan}{x}}−\sqrt{\mathrm{cot}{x}}\right){dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{tan}{x}−\mathrm{1}}{\:\sqrt{\mathrm{tan}{x}}}{dx},\:\mathrm{tan}{x}={u}^{\mathrm{2}} \Rightarrow\mathrm{2}{udu}=\left(\mathrm{1}+{u}^{\mathrm{4}} \right){dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}}\centerdot\frac{\mathrm{2}{u}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}=\sqrt{\mathrm{2}}\int\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}=\sqrt{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{{u}^{\mathrm{2}} +\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{du} \\ $$$$\:\:\:=\sqrt{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{\left({u}−\frac{\mathrm{1}}{{u}}\right)^{\mathrm{2}} +\mathrm{2}}{du}=\sqrt{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}=\mathrm{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$\:\:\:=\mathrm{arctan}\left(\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{2}}{u}}\right)+{C}=\mathrm{arctan}\left(\frac{\mathrm{tan}{x}−\mathrm{1}}{\:\sqrt{\mathrm{2tan}{x}}}\right)+{C} \\ $$
Answered by Ar Brandon last updated on 21/Dec/21

$$\mathrm{cos7}{x}\mathrm{cos17}{x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos24}{x}+\mathrm{cos10}{x}\right) \\ $$$$\mathrm{cos7}{x}\mathrm{cos17}{x}\mathrm{cos37}{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos61}{x}+\mathrm{cos13}{x}+\mathrm{cos47}{x}+\mathrm{cos27}{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos7}{x}\mathrm{cos17}{x}\mathrm{cos37}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{sin61}{x}}{\mathrm{61}}+\frac{\mathrm{sin13}{x}}{\mathrm{13}}+\frac{\mathrm{sin47}{x}}{\mathrm{47}}+\frac{\mathrm{sin27}{x}}{\mathrm{27}}\right)_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{61}}+\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{47}}−\frac{\mathrm{1}}{\mathrm{27}}\right) \\ $$
