Menu Close

solve-inside-C-x-1-x-3-x-1-x-2-x-1-x-1-0-

Tinku Tara 0 Comments
Pin




Question Number 96211 by mathmax by abdo last updated on 30/May/20
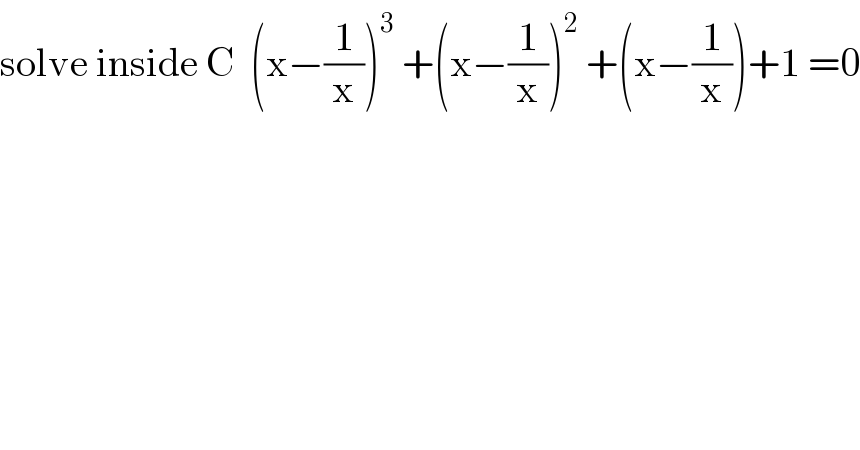
solve inside C (x−(1/x))^3 +(x−(1/x))^2 +(x−(1/x))+1 =0
$$\mathrm{solve}\:\mathrm{inside}\:\mathrm{C}\:\:\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{3}} \:+\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} \:+\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{1}\:=\mathrm{0} \\ $$
Answered by mr W last updated on 30/May/20
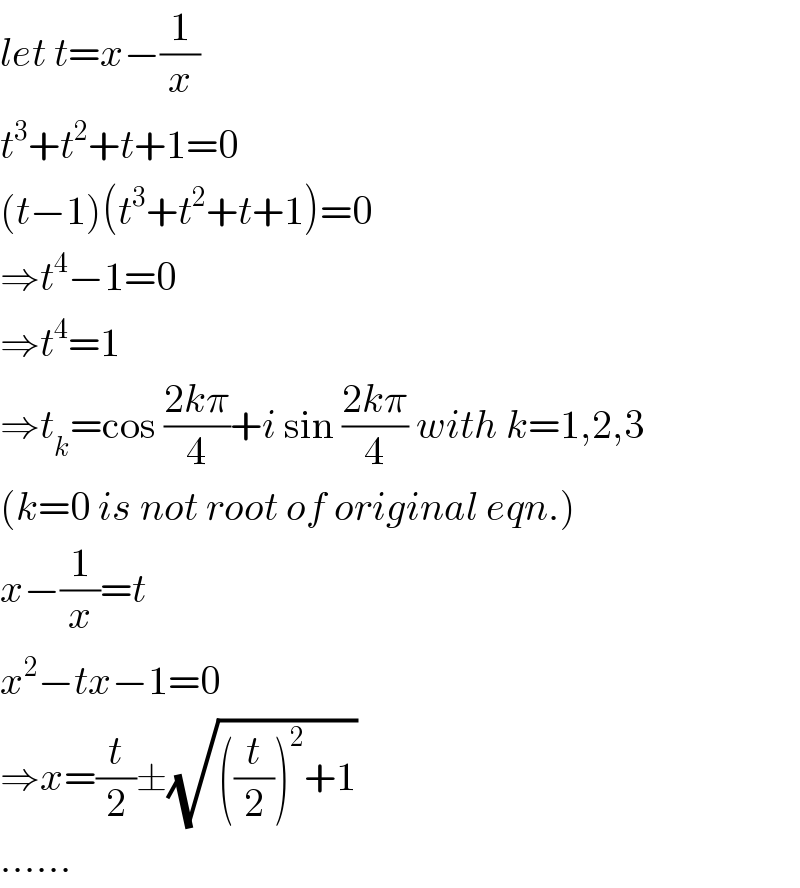
let t=x−(1/x) t^3 +t^2 +t+1=0 (t−1)(t^3 +t^2 +t+1)=0 ⇒t^4 −1=0 ⇒t^4 =1 ⇒t_k =cos ((2kπ)/4)+i sin ((2kπ)/4) with k=1,2,3 (k=0 is not root of original eqn.) x−(1/x)=t x^2 −tx−1=0 ⇒x=(t/2)±(√(((t/2))^2 +1)) ......
$${let}\:{t}={x}−\frac{\mathrm{1}}{{x}} \\ $$$${t}^{\mathrm{3}} +{t}^{\mathrm{2}} +{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{3}} +{t}^{\mathrm{2}} +{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{4}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{4}} =\mathrm{1} \\ $$$$\Rightarrow{t}_{{k}} =\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{\mathrm{4}}+{i}\:\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{\mathrm{4}}\:{with}\:{k}=\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\left({k}=\mathrm{0}\:{is}\:{not}\:{root}\:{of}\:{original}\:{eqn}.\right) \\ $$$${x}−\frac{\mathrm{1}}{{x}}={t} \\ $$$${x}^{\mathrm{2}} −{tx}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{{t}}{\mathrm{2}}\pm\sqrt{\left(\frac{{t}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$…… \\ $$
Answered by mathmax by abdo last updated on 30/May/20
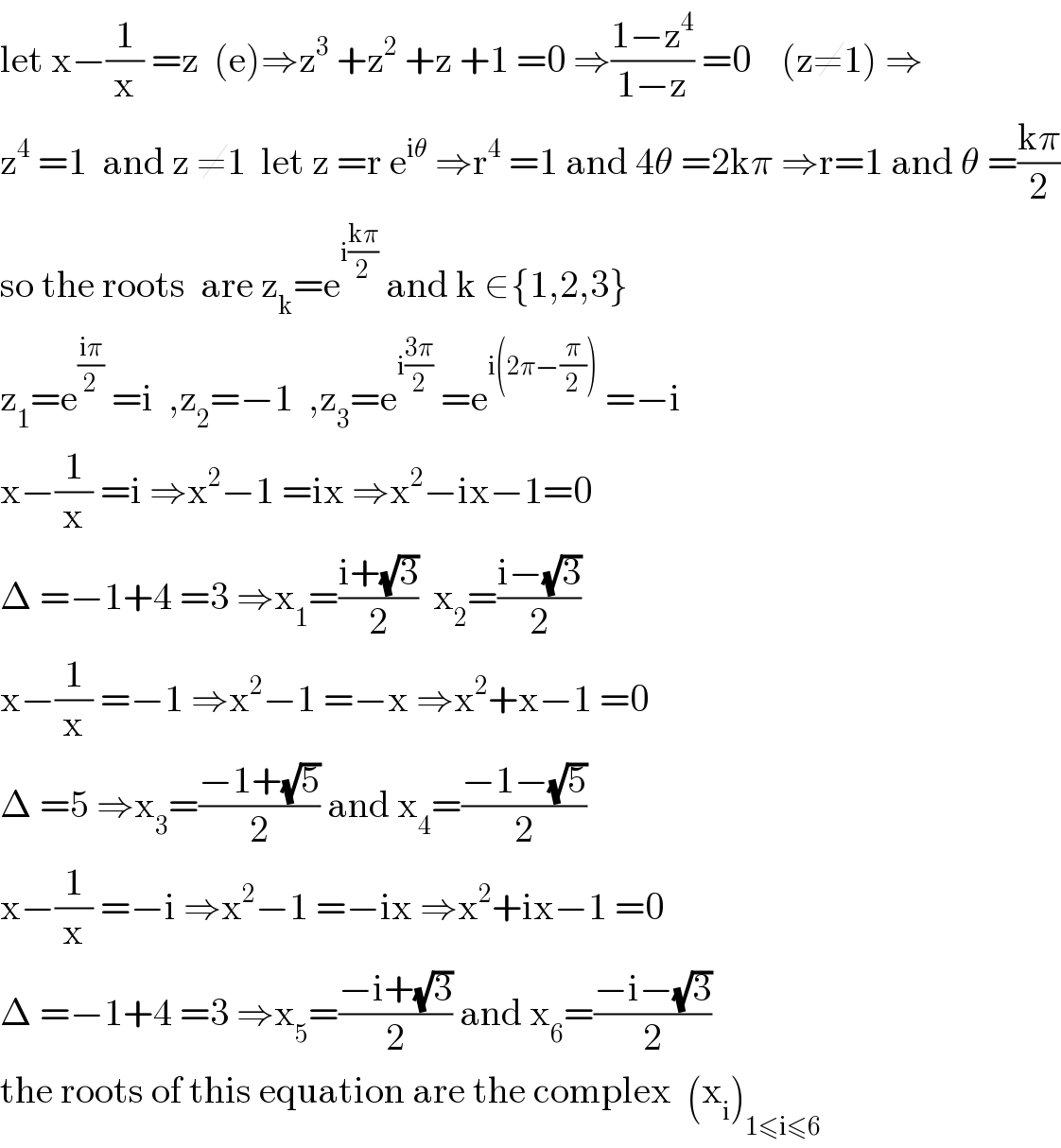
let x−(1/x) =z (e)⇒z^3 +z^2 +z +1 =0 ⇒((1−z^4 )/(1−z)) =0 (z≠1) ⇒ z^4 =1 and z ≠1 let z =r e^(iθ) ⇒r^4 =1 and 4θ =2kπ ⇒r=1 and θ =((kπ)/2) so the roots are z_k =e^(i((kπ)/2)) and k ∈{1,2,3} z_1 =e^((iπ)/2) =i ,z_2 =−1 ,z_3 =e^(i((3π)/2)) =e^(i(2π−(π/2))) =−i x−(1/x) =i ⇒x^2 −1 =ix ⇒x^2 −ix−1=0 Δ =−1+4 =3 ⇒x_1 =((i+(√3))/2) x_2 =((i−(√3))/2) x−(1/x) =−1 ⇒x^2 −1 =−x ⇒x^2 +x−1 =0 Δ =5 ⇒x_3 =((−1+(√5))/2) and x_4 =((−1−(√5))/2) x−(1/x) =−i ⇒x^2 −1 =−ix ⇒x^2 +ix−1 =0 Δ =−1+4 =3 ⇒x_5 =((−i+(√3))/2) and x_6 =((−i−(√3))/2) the roots of this equation are the complex (x_i )_(1≤i≤6)
$$\mathrm{let}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{z}\:\:\left(\mathrm{e}\right)\Rightarrow\mathrm{z}^{\mathrm{3}} \:+\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}\:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}−\mathrm{z}^{\mathrm{4}} }{\mathrm{1}−\mathrm{z}}\:=\mathrm{0}\:\:\:\:\left(\mathrm{z}\neq\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{z}^{\mathrm{4}} \:=\mathrm{1}\:\:\mathrm{and}\:\mathrm{z}\:\neq\mathrm{1}\:\:\mathrm{let}\:\mathrm{z}\:=\mathrm{r}\:\mathrm{e}^{\mathrm{i}\theta} \:\Rightarrow\mathrm{r}^{\mathrm{4}} \:=\mathrm{1}\:\mathrm{and}\:\mathrm{4}\theta\:=\mathrm{2k}\pi\:\Rightarrow\mathrm{r}=\mathrm{1}\:\mathrm{and}\:\theta\:=\frac{\mathrm{k}\pi}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{roots}\:\:\mathrm{are}\:\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{k}\pi}{\mathrm{2}}} \:\mathrm{and}\:\mathrm{k}\:\in\left\{\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$$\mathrm{z}_{\mathrm{1}} =\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \:=\mathrm{i}\:\:,\mathrm{z}_{\mathrm{2}} =−\mathrm{1}\:\:,\mathrm{z}_{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{2}}} \:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2}\pi−\frac{\pi}{\mathrm{2}}\right)} \:=−\mathrm{i} \\ $$$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{i}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:=\mathrm{ix}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{ix}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta\:=−\mathrm{1}+\mathrm{4}\:=\mathrm{3}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{i}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{i}−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\:=−\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:=−\mathrm{x}\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{5}\:\Rightarrow\mathrm{x}_{\mathrm{3}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{x}_{\mathrm{4}} =\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\:=−\mathrm{i}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:=−\mathrm{ix}\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{ix}−\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=−\mathrm{1}+\mathrm{4}\:=\mathrm{3}\:\Rightarrow\mathrm{x}_{\mathrm{5}} =\frac{−\mathrm{i}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{x}_{\mathrm{6}} =\frac{−\mathrm{i}−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{are}\:\mathrm{the}\:\mathrm{complex}\:\:\left(\mathrm{x}_{\mathrm{i}} \right)_{\mathrm{1}\leqslant\mathrm{i}\leqslant\mathrm{6}} \\ $$
Answered by MJS last updated on 30/May/20
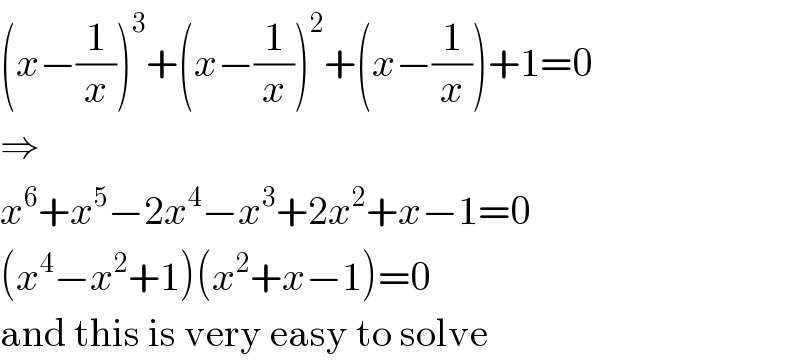
(x−(1/x))^3 +(x−(1/x))^2 +(x−(1/x))+1=0 ⇒ x^6 +x^5 −2x^4 −x^3 +2x^2 +x−1=0 (x^4 −x^2 +1)(x^2 +x−1)=0 and this is very easy to solve
$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} +\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left({x}−\frac{\mathrm{1}}{{x}}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{6}} +{x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{very}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by mr W last updated on 30/May/20
good idea!
$${good}\:{idea}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *