Question Number 30760 by abdo imad last updated on 25/Feb/18
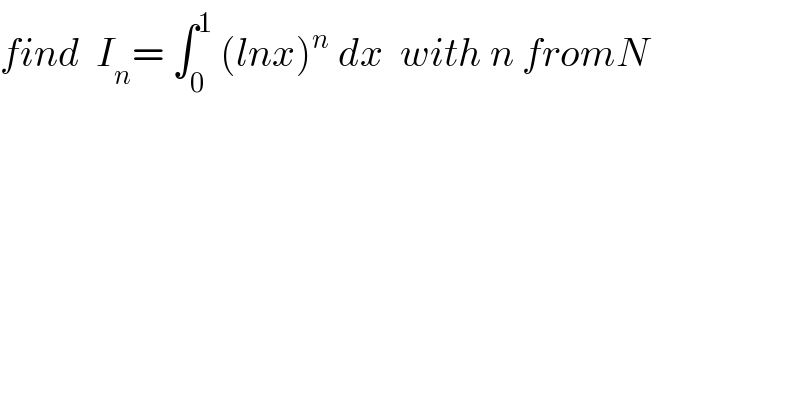
$${find}\:\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({lnx}\right)^{{n}} \:{dx}\:\:{with}\:{n}\:{fromN} \\ $$
Commented by abdo imad last updated on 27/Feb/18
![the ch. lnx=−t give I_n = −∫_0 ^(+∞) (−t)^n (−e^(−t) )dt =(−1)^n ∫_0 ^∞ t^n e^(−t) dt =(−1)^n A_(n ) let integrate by parts A_n =[−t^n e^(−t) ]_0 ^∞ −∫_0 ^∞ −nt^(n−1) e^(−t) dt =n∫_0 ^∞ t^(n−1) e^(−t) dt =nA_(n−1) ⇒Π_(k=1) ^n A_k = Π_(k=1) ^n k.Π_(k=1) ^n A_(k−1) ⇒ A_1 .A_2 ....A_n =n! A_0 A_1 ....A_(n−1) ⇒A_n =n! A_0 =n! ⇒ I_n =(−1)^n n! .](https://www.tinkutara.com/question/Q30886.png)
$${the}\:{ch}.\:{lnx}=−{t}\:{give}\:\:{I}_{{n}} =\:−\int_{\mathrm{0}} ^{+\infty} \:\left(−{t}\right)^{{n}} \left(−\boldsymbol{{e}}^{−\boldsymbol{{t}}} \right)\boldsymbol{{dt}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} {e}^{−{t}} {dt}\:=\left(−\mathrm{1}\right)^{{n}} \:{A}_{{n}\:} \:{let}\:{integrate}\:{by}\:{parts} \\ $$$${A}_{{n}} =\left[−{t}^{{n}} {e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} −{nt}^{{n}−\mathrm{1}} \:{e}^{−{t}} {dt}\:={n}\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}−\mathrm{1}} \:{e}^{−{t}} {dt} \\ $$$$={nA}_{{n}−\mathrm{1}} \:\:\Rightarrow\prod_{{k}=\mathrm{1}} ^{{n}} \:{A}_{{k}} =\:\prod_{{k}=\mathrm{1}} ^{{n}} {k}.\prod_{{k}=\mathrm{1}} ^{{n}} \:{A}_{{k}−\mathrm{1}} \:\Rightarrow \\ $$$${A}_{\mathrm{1}} .{A}_{\mathrm{2}} ….{A}_{{n}} ={n}!\:{A}_{\mathrm{0}} \:{A}_{\mathrm{1}} ….{A}_{{n}−\mathrm{1}} \:\Rightarrow{A}_{{n}} ={n}!\:{A}_{\mathrm{0}} ={n}!\:\Rightarrow \\ $$$${I}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}!\:\:. \\ $$
