Question Number 96346 by Ar Brandon last updated on 31/May/20

$$\int\frac{\mathrm{1}}{\mathfrak{ln}\left(\mathfrak{x}\right)}\boldsymbol{\mathrm{d}}\mathfrak{x} \\ $$
Commented by Tony Lin last updated on 01/Jun/20
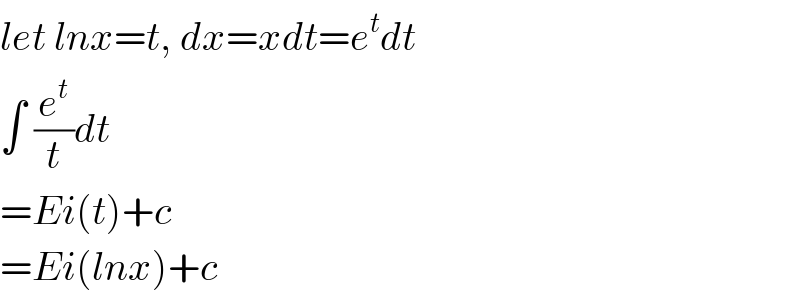
$${let}\:{lnx}={t},\:{dx}={xdt}={e}^{{t}} {dt} \\ $$$$\int\:\frac{{e}^{{t}} }{{t}}{dt} \\ $$$$={Ei}\left({t}\right)+{c} \\ $$$$={Ei}\left({lnx}\right)+{c} \\ $$
Commented by Sourav mridha last updated on 01/Jun/20
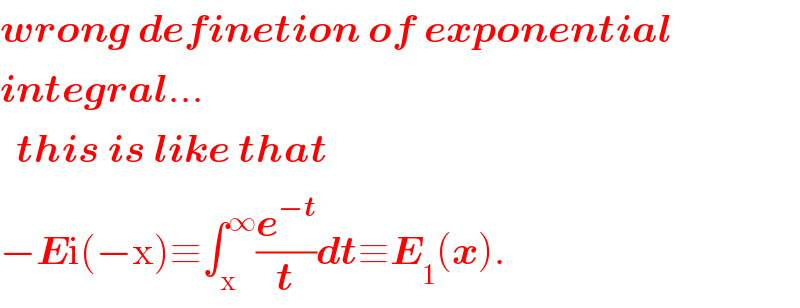
$$\boldsymbol{{wrong}}\:\boldsymbol{{definetion}}\:\boldsymbol{{of}}\:\boldsymbol{{exponential}} \\ $$$$\boldsymbol{{integral}}… \\ $$$$\:\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{like}}\:\boldsymbol{{that}}\:\: \\ $$$$−\boldsymbol{{E}}\mathrm{i}\left(−\mathrm{x}\right)\equiv\int_{\mathrm{x}} ^{\infty} \frac{\boldsymbol{{e}}^{−\boldsymbol{{t}}} }{\boldsymbol{{t}}}\boldsymbol{{dt}}\equiv\boldsymbol{{E}}_{\mathrm{1}} \left(\boldsymbol{{x}}\right). \\ $$
Commented by Tony Lin last updated on 02/Jun/20
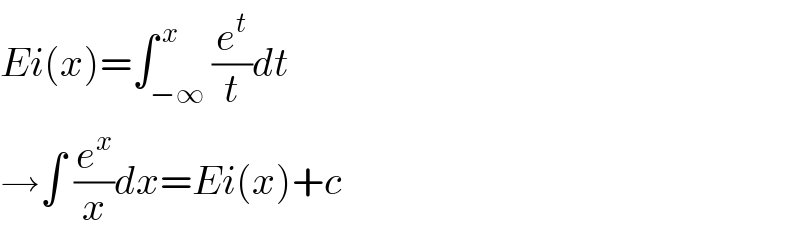
$${Ei}\left({x}\right)=\int_{−\infty} ^{\:{x}} \frac{{e}^{{t}} }{{t}}{dt} \\ $$$$\rightarrow\int\:\frac{{e}^{{x}} }{{x}}{dx}={Ei}\left({x}\right)+{c} \\ $$
Commented by Tony Lin last updated on 02/Jun/20

$$\int\frac{\mathrm{1}}{{lnx}}{dx} \\ $$$$={li}\left({x}\right)+{c} \\ $$
Answered by niroj last updated on 01/Jun/20
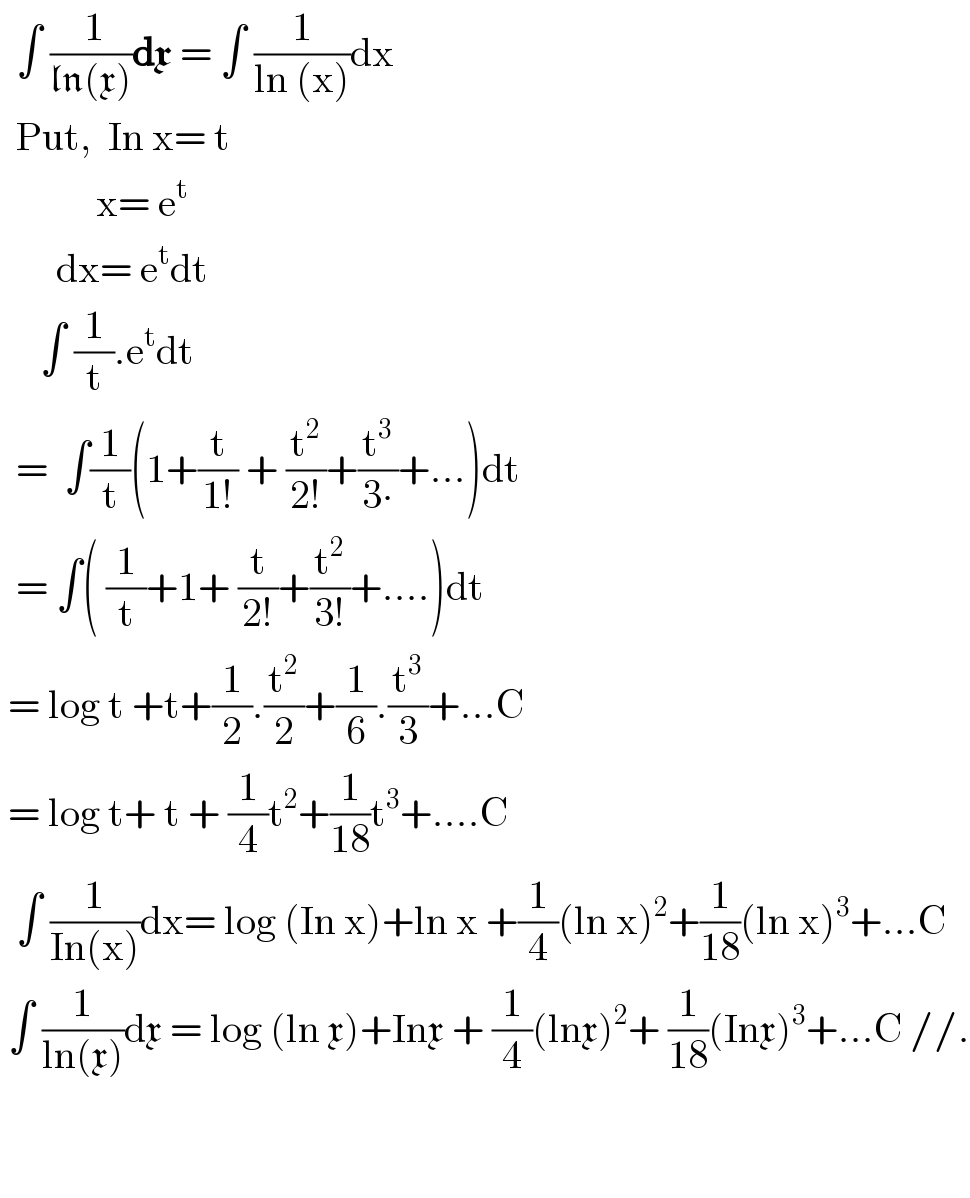
$$\:\:\int\:\frac{\:\mathrm{1}}{\mathfrak{ln}\left(\mathfrak{x}\right)}\boldsymbol{\mathrm{d}\mathfrak{x}}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{ln}\:\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\:\:\mathrm{Put},\:\:\mathrm{In}\:\mathrm{x}=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\:\mathrm{e}^{\mathrm{t}} \\ $$$$\:\:\:\:\:\:\:\mathrm{dx}=\:\mathrm{e}^{\mathrm{t}} \mathrm{dt} \\ $$$$\:\:\:\:\:\int\:\frac{\mathrm{1}}{\mathrm{t}}.\mathrm{e}^{\mathrm{t}} \mathrm{dt} \\ $$$$\:\:=\:\:\int\frac{\mathrm{1}}{\mathrm{t}}\left(\mathrm{1}+\frac{\mathrm{t}}{\mathrm{1}!}\:+\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}\centerdot}+…\right)\mathrm{dt} \\ $$$$\:\:=\:\int\left(\:\frac{\mathrm{1}}{\mathrm{t}}+\mathrm{1}+\:\frac{\mathrm{t}}{\mathrm{2}!}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{3}!}+….\right)\mathrm{dt} \\ $$$$\:=\:\mathrm{log}\:\mathrm{t}\:+\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}.\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}+…\mathrm{C} \\ $$$$\:=\:\mathrm{log}\:\mathrm{t}+\:\mathrm{t}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{18}}\mathrm{t}^{\mathrm{3}} +….\mathrm{C} \\ $$$$\:\:\int\:\frac{\mathrm{1}}{\mathrm{In}\left(\mathrm{x}\right)}\mathrm{dx}=\:\mathrm{log}\:\left(\mathrm{In}\:\mathrm{x}\right)+\mathrm{ln}\:\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{ln}\:\mathrm{x}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{18}}\left(\mathrm{ln}\:\mathrm{x}\right)^{\mathrm{3}} +…\mathrm{C} \\ $$$$\:\int\:\frac{\mathrm{1}}{\mathrm{ln}\left(\mathfrak{x}\right)}\mathrm{d}\mathfrak{x}\:=\:\mathrm{log}\:\left(\mathrm{ln}\:\mathfrak{x}\right)+\mathrm{In}\mathfrak{x}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{ln}\mathfrak{x}\right)^{\mathrm{2}} +\:\frac{\mathrm{1}}{\mathrm{18}}\left(\mathrm{In}\mathfrak{x}\right)^{\mathrm{3}} +…\mathrm{C}\://. \\ $$$$\: \\ $$$$\:\: \\ $$
Commented by Ar Brandon last updated on 01/Jun/20
Thank you Mr niroj, ��
Commented by Mr.D.N. last updated on 01/Jun/20
������
