Question Number 248 by sushmitak last updated on 25/Jan/15
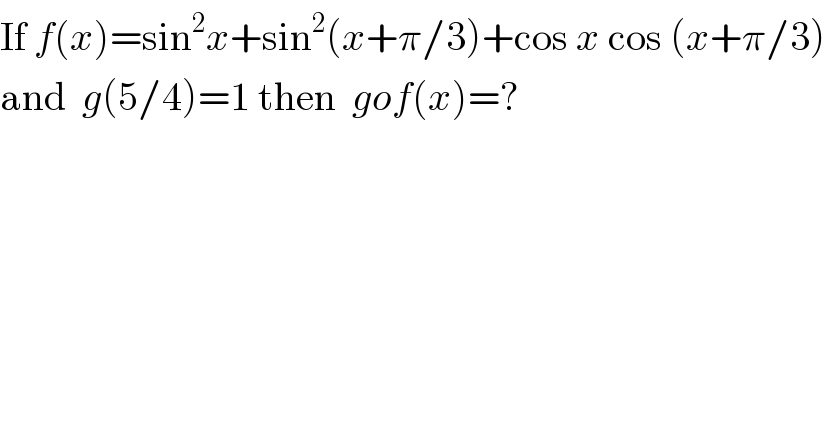
$$\mathrm{If}\:{f}\left({x}\right)=\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} \left({x}+\pi/\mathrm{3}\right)+\mathrm{cos}\:{x}\:\mathrm{cos}\:\left({x}+\pi/\mathrm{3}\right) \\ $$$$\mathrm{and}\:\:{g}\left(\mathrm{5}/\mathrm{4}\right)=\mathrm{1}\:\mathrm{then}\:\:{gof}\left({x}\right)=? \\ $$
Answered by 123456 last updated on 17/Dec/14
![f(x)=sin^2 x+sin^2 (x+(π/3))+cos x cos(x+(π/3)) cos (x+(π/3))=cos x cos(π/3)−sin x sin (π/3) =(1/2)cos x−((√3)/2)sin x cos x cos (x+(π/3))=(1/2)cos^2 x−((√3)/2)cos x sin x sin (x+(π/3))=sin x cos (π/3)+cos x sin (π/3) =(1/2)sin x+((√3)/2)cos x sin^2 (x+(π/3))=(1/4)sin^2 x+((√3)/2)cos x sin x+(3/4)cos^2 x f(x)=sin^2 x+sin^2 (x+(π/3))+cos x cos(x+(π/3)) =sin^2 x+(1/4)sin^2 x+((√3)/2)cos x sin x+(3/4)cos^2 x+(1/2)cos^2 x−((√3)/2)cos x sin x =(1+(1/4))sin^2 x+((3/4)+(1/2))cos^2 x =(5/4)sin^2 x+(5/4)cos^2 x =(5/4)(sin^2 x+cos^2 x)=(5/4) then g[f(x)]=g((5/4))=1](https://www.tinkutara.com/question/Q249.png)
$${f}\left({x}\right)=\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} \left({x}+\frac{\pi}{\mathrm{3}}\right)+\mathrm{cos}\:{x}\:\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{3}}\right)=\mathrm{cos}\:{x}\:\mathrm{cos}\frac{\pi}{\mathrm{3}}−\mathrm{sin}\:{x}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{x} \\ $$$$\mathrm{cos}\:{x}\:\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} {x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\:\mathrm{sin}\:{x} \\ $$$$\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{3}}\right)=\mathrm{sin}\:{x}\:\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+\mathrm{cos}\:{x}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x} \\ $$$$\mathrm{sin}^{\mathrm{2}} \left({x}+\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} {x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:^{\mathrm{2}} {x} \\ $$$${f}\left({x}\right)=\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} \left({x}+\frac{\pi}{\mathrm{3}}\right)+\mathrm{cos}\:{x}\:\mathrm{cos}\left({x}+\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{sin}^{\mathrm{2}} {x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} {x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}^{\mathrm{2}} {x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} {x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\:\mathrm{sin}\:{x} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{sin}^{\mathrm{2}} {x}+\left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{cos}^{\mathrm{2}} {x} \\ $$$$=\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} {x}+\frac{\mathrm{5}}{\mathrm{4}}\mathrm{cos}^{\mathrm{2}} {x} \\ $$$$=\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{sin}^{\mathrm{2}} \boldsymbol{{x}}+\mathrm{cos}^{\mathrm{2}} \boldsymbol{{x}}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{then}} \\ $$$${g}\left[{f}\left({x}\right)\right]={g}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)=\mathrm{1} \\ $$
