Question Number 30855 by anunil1234 last updated on 27/Feb/18
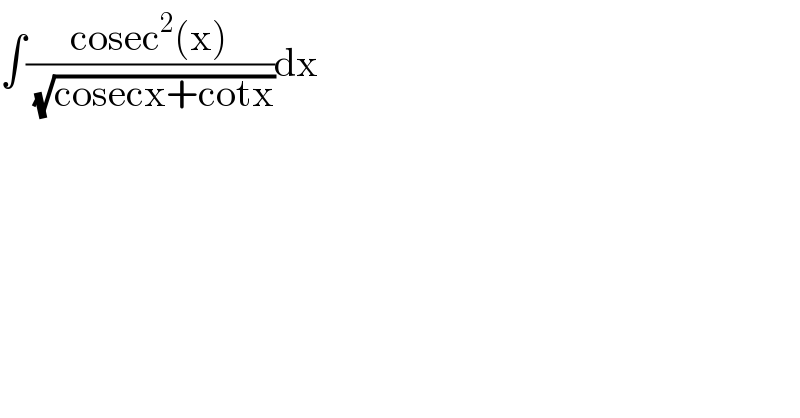
$$\int\frac{\mathrm{cosec}^{\mathrm{2}} \left(\mathrm{x}\right)}{\:\sqrt{\mathrm{cosecx}+\mathrm{cotx}}}\mathrm{dx} \\ $$
Answered by math1967 last updated on 03/Mar/18
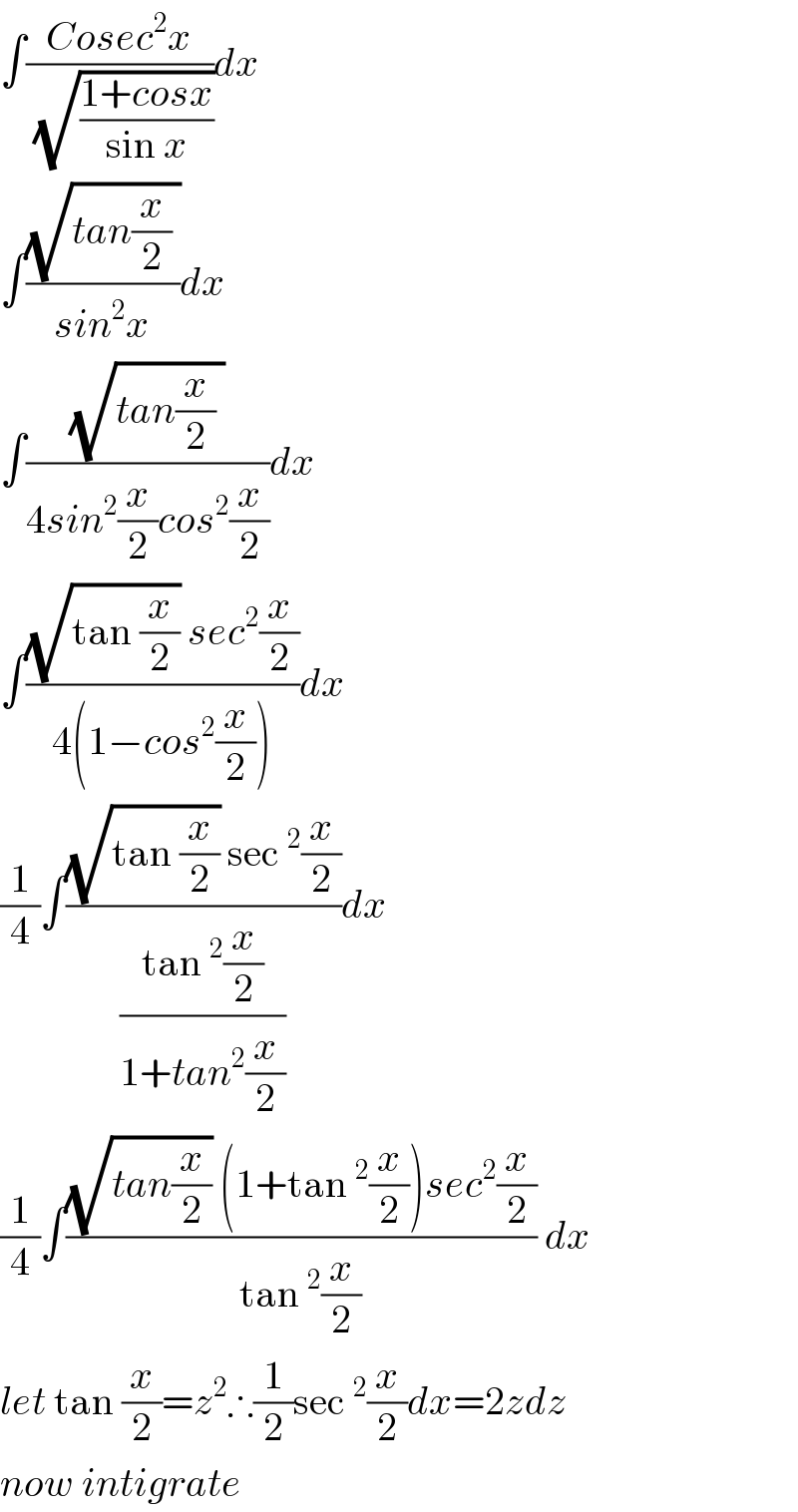
$$\int\frac{{Cosec}^{\mathrm{2}} {x}}{\:\sqrt{\frac{\mathrm{1}+{cosx}}{\mathrm{sin}\:{x}}}}{dx} \\ $$$$\int\frac{\sqrt{{tan}\frac{{x}}{\mathrm{2}}\:}}{{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$\int\frac{\sqrt{{tan}\frac{{x}}{\mathrm{2}}\:}}{\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\int\frac{\sqrt{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}\:{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{4}\left(\mathrm{1}−{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\sqrt{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}\:\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\sqrt{{tan}\frac{{x}}{\mathrm{2}}}\:\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right){sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\:{dx} \\ $$$${let}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}={z}^{\mathrm{2}} \therefore\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}=\mathrm{2}{zdz} \\ $$$${now}\:{intigrate} \\ $$
