Question Number 96392 by john santu last updated on 01/Jun/20
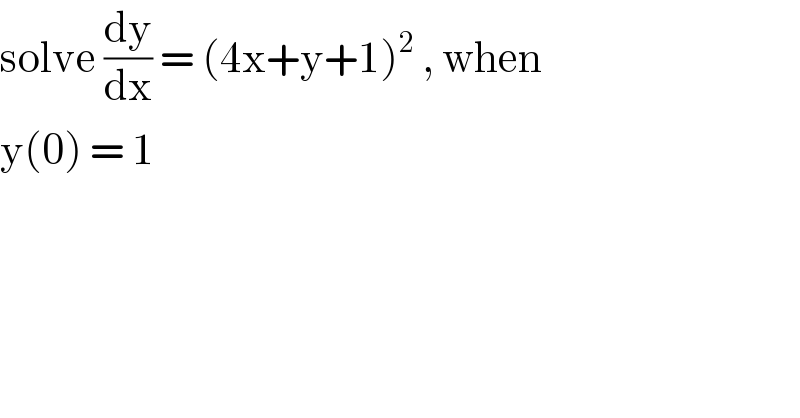
$$\mathrm{solve}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\left(\mathrm{4x}+\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} \:,\:\mathrm{when}\: \\ $$$$\mathrm{y}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$
Answered by bobhans last updated on 01/Jun/20
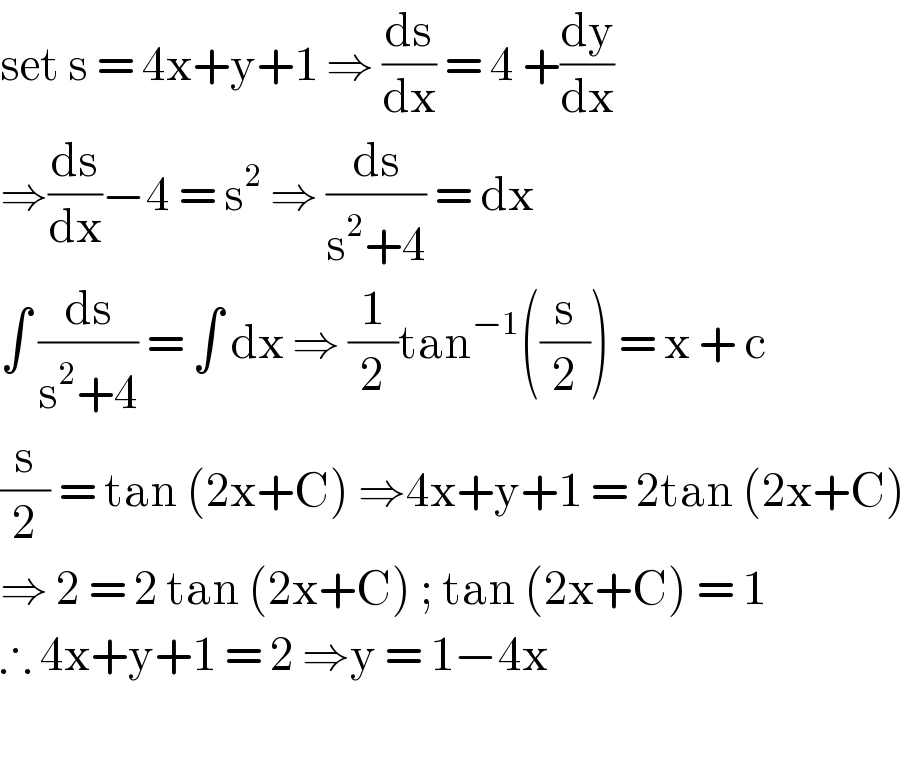
$$\mathrm{set}\:\mathrm{s}\:=\:\mathrm{4x}+\mathrm{y}+\mathrm{1}\:\Rightarrow\:\frac{\mathrm{ds}}{\mathrm{dx}}\:=\:\mathrm{4}\:+\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\Rightarrow\frac{\mathrm{ds}}{\mathrm{dx}}−\mathrm{4}\:=\:\mathrm{s}^{\mathrm{2}} \:\Rightarrow\:\frac{\mathrm{ds}}{\mathrm{s}^{\mathrm{2}} +\mathrm{4}}\:=\:\mathrm{dx}\: \\ $$$$\int\:\frac{\mathrm{ds}}{\mathrm{s}^{\mathrm{2}} +\mathrm{4}}\:=\:\int\:\mathrm{dx}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{s}}{\mathrm{2}}\right)\:=\:\mathrm{x}\:+\:\mathrm{c} \\ $$$$\frac{\mathrm{s}}{\mathrm{2}}\:=\:\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{C}\right)\:\Rightarrow\mathrm{4x}+\mathrm{y}+\mathrm{1}\:=\:\mathrm{2tan}\:\left(\mathrm{2x}+\mathrm{C}\right) \\ $$$$\Rightarrow\:\mathrm{2}\:=\:\mathrm{2}\:\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{C}\right)\:;\:\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{C}\right)\:=\:\mathrm{1} \\ $$$$\therefore\:\mathrm{4x}+\mathrm{y}+\mathrm{1}\:=\:\mathrm{2}\:\Rightarrow\mathrm{y}\:=\:\mathrm{1}−\mathrm{4x}\: \\ $$$$ \\ $$
