Question Number 133957 by mathmax by abdo last updated on 25/Feb/21
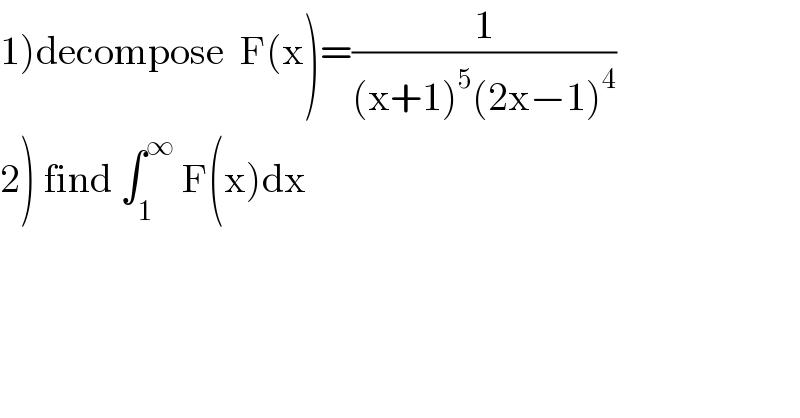
$$\left.\mathrm{1}\right)\mathrm{decompose}\:\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\int_{\mathrm{1}} ^{\infty} \:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by Olaf last updated on 25/Feb/21
![F(x) = (1/((x+1)^5 (2x−1)^4 )) F(x) = (1/(81(x+1)^5 ))+(8/(243(x+1)^4 ))+((40)/(729(x+1)^3 )) +((160)/(2187(x+1)^2 ))+((570)/(6561(x+1)))+(2/(243(x−(1/2))^4 )) −((20)/(729(x−(1/2))^3 ))+((40)/(729(x−(1/2))^2 ))−((560)/(6561(x−(1/2)))) ∫_1 ^∞ F(x)dx = [−(1/(324(x+1)^4 ))−(8/(729(x+1)^3 )) −((20)/(729(x+1)^2 ))−((160)/(2187(x+1)))+((570)/(6561))ln(x+1) −(2/(729(x−(1/2))^3 ))+((10)/(729(x−(1/2))^2 ))−((40)/(729(x−(1/2)))) −((560)/(6561))ln(x−(1/2))]_1 ^∞ = ((27051)/(139968))−((1120)/(6561))ln2](https://www.tinkutara.com/question/Q133962.png)
$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{81}\left({x}+\mathrm{1}\right)^{\mathrm{5}} }+\frac{\mathrm{8}}{\mathrm{243}\left({x}+\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{40}}{\mathrm{729}\left({x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$+\frac{\mathrm{160}}{\mathrm{2187}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{570}}{\mathrm{6561}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{243}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$$$−\frac{\mathrm{20}}{\mathrm{729}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }+\frac{\mathrm{40}}{\mathrm{729}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{560}}{\mathrm{6561}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$ \\ $$$$\int_{\mathrm{1}} ^{\infty} \mathrm{F}\left({x}\right){dx}\:=\:\left[−\frac{\mathrm{1}}{\mathrm{324}\left({x}+\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{8}}{\mathrm{729}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\right. \\ $$$$−\frac{\mathrm{20}}{\mathrm{729}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{160}}{\mathrm{2187}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{570}}{\mathrm{6561}}\mathrm{ln}\left({x}+\mathrm{1}\right) \\ $$$$−\frac{\mathrm{2}}{\mathrm{729}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }+\frac{\mathrm{10}}{\mathrm{729}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{40}}{\mathrm{729}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\left.−\frac{\mathrm{560}}{\mathrm{6561}}\mathrm{ln}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\:\frac{\mathrm{27051}}{\mathrm{139968}}−\frac{\mathrm{1120}}{\mathrm{6561}}\mathrm{ln2} \\ $$
Commented by mathmax by abdo last updated on 26/Feb/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 27/Feb/21
![2)Φ=∫_1 ^∞ (dx/((x+1)^5 (2x−1)^4 )) ⇒Φ =∫_1 ^∞ (dx/((((x+1)/(2x−1)))^5 (2x−1)^9 )) we do the changement ((x+1)/(2x−1))=t ⇒x+1=2tx−t ⇒(1−2t)x=−1−t ⇒ x=((−1−t)/(1−2t)) =((t+1)/(2t−1)) ⇒(dx/dt)=((2t−1−2(t+1))/((2t−1)^2 ))=((−3)/((2t−1)^2 )) and 2x−1 =((2t+2)/(2t−1))−1 =((2t+2−2t+1)/(2t−1)) =(3/(2t−1)) ⇒ Φ =∫_2 ^(1/2) (1/(t^5 ((3/(2t−1)))^9 ))((−3dt)/((2t−1)^2 )) =(1/3^8 )∫_(1/2) ^2 (((2t−1)^9 )/((2t−1)^2 t^5 ))dt =(1/3^8 )∫_(1/2) ^2 (((2t−1)^7 )/t^5 )dt ⇒3^8 Φ =∫_(1/2) ^2 (1/t^5 )Σ_(k=0) ^7 C_7 ^k (2t)^k (−1)^(7−k) =−Σ_(k=0) ^7 2^k (−1)^k C_7 ^k ∫_(1/2) ^2 t^(k−5) dt =−Σ_(k=0 and k≠4) ^7 (−2)^k C_7 ^k [(1/(k−4))t^(k−4) ]_(1/2) ^2 −(−2)^4 C_7 ^4 [ln∣t∣]_(1/2) ^2 =−Σ_(k=0 and k≠4) ^7 (−2)^k (C_7 ^k /(k−4))(2^(k−4) −(1/2^(k−4) ))−2^4 C_7 ^4 (2ln2) ⇒ Φ =−(1/3^8 ){ Σ_(k=0 and k≠4) ^7 (((−2)^k C_7 ^k )/(k−4))(2^(k−4) −(1/2^(k−4) ))+2^5 ln(2)C_7 ^4 }](https://www.tinkutara.com/question/Q134084.png)
$$\left.\mathrm{2}\right)\Phi=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{4}} }\:\Rightarrow\Phi\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{5}} \left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{9}} } \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}−\mathrm{1}}=\mathrm{t}\:\Rightarrow\mathrm{x}+\mathrm{1}=\mathrm{2tx}−\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{2t}\right)\mathrm{x}=−\mathrm{1}−\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{x}=\frac{−\mathrm{1}−\mathrm{t}}{\mathrm{1}−\mathrm{2t}}\:=\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2t}−\mathrm{1}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{2t}−\mathrm{1}−\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{−\mathrm{3}}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{and} \\ $$$$\mathrm{2x}−\mathrm{1}\:=\frac{\mathrm{2t}+\mathrm{2}}{\mathrm{2t}−\mathrm{1}}−\mathrm{1}\:=\frac{\mathrm{2t}+\mathrm{2}−\mathrm{2t}+\mathrm{1}}{\mathrm{2t}−\mathrm{1}}\:=\frac{\mathrm{3}}{\mathrm{2t}−\mathrm{1}}\:\Rightarrow \\ $$$$\Phi\:=\int_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} \left(\frac{\mathrm{3}}{\mathrm{2t}−\mathrm{1}}\right)^{\mathrm{9}} }\frac{−\mathrm{3dt}}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \:\frac{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{9}} }{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{5}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \:\frac{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{5}} }\mathrm{dt}\:\Rightarrow\mathrm{3}^{\mathrm{8}} \:\Phi\:=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \left(\mathrm{2t}\right)^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{7}−\mathrm{k}} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \:\mathrm{2}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \:\mathrm{t}^{\mathrm{k}−\mathrm{5}} \:\mathrm{dt} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{4}} ^{\mathrm{7}} \:\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{k}−\mathrm{4}}\mathrm{t}^{\mathrm{k}−\mathrm{4}} \right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} −\left(−\mathrm{2}\right)^{\mathrm{4}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{4}} \left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{4}} ^{\mathrm{7}} \:\left(−\mathrm{2}\right)^{\mathrm{k}} \:\frac{\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{4}}\left(\mathrm{2}^{\mathrm{k}−\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{4}} }\right)−\mathrm{2}^{\mathrm{4}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{4}} \left(\mathrm{2ln2}\right)\:\Rightarrow \\ $$$$\Phi\:=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{8}} }\left\{\:\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{4}} ^{\mathrm{7}} \:\frac{\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{4}}\left(\mathrm{2}^{\mathrm{k}−\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{4}} }\right)+\mathrm{2}^{\mathrm{5}} \mathrm{ln}\left(\mathrm{2}\right)\mathrm{C}_{\mathrm{7}} ^{\mathrm{4}} \right\} \\ $$
