Question Number 30862 by ajfour last updated on 27/Feb/18

Answered by mrW2 last updated on 27/Feb/18
![(a/(sin A))=(b/(sin B))=(c/(sin C))=(1/λ)=2R=((abc)/(2(√(s(s−a)(s−b)(s−c))))) ((BQ)/(sin (C−θ)))=((CQ)/(sin θ))=((BC)/(sin (π−θ−C+θ))) ((BQ)/(sin (C−θ)))=((CQ)/(sin θ))=(a/(sin C)) ⇒BQ=((sin (C−θ))/(sin C))×a ⇒CQ=((sin θ)/(sin C))×a similarly ⇒BP=((sin θ)/(sin B))×c ⇒a′=PQ=BQ−BP=((sin (C−θ))/(sin C))×a−((sin θ)/(sin B))×c ⇒a′=((cλ cos θ−cos C sin θ)/(cλ))×a−((sin θ)/(bλ))×c ⇒a′=a cos θ−(((ab cos C+c^2 ) sin θ)/(bcλ)) ⇒a′=a cos θ−(((((a^2 +b^2 −c^2 )/2)+c^2 ) sin θ)/(bcλ)) ⇒a′=a cos θ−(((a^2 +b^2 +c^2 ) sin θ)/(2bcλ)) ⇒a′=[cos θ−(((a^2 +b^2 +c^2 ) sin θ)/(4(√(s(s−a)(s−b)(s−c)))))]a=k a similarly ⇒b′=k b ⇒c′=k c ⇒r=k r_(ΔABC) =k ((√(s(s−a)(s−b)(s−c)))/s) ⇒r=[cos θ−(((a^2 +b^2 +c^2 ) sin θ)/(4(√(s(s−a)(s−b)(s−c)))))]×(√(((s−a)(s−b)(s−c))/s))](https://www.tinkutara.com/question/Q30867.png)
$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\frac{\mathrm{1}}{\lambda}=\mathrm{2}{R}=\frac{{abc}}{\mathrm{2}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}} \\ $$$$\frac{{BQ}}{\mathrm{sin}\:\left({C}−\theta\right)}=\frac{{CQ}}{\mathrm{sin}\:\theta}=\frac{{BC}}{\mathrm{sin}\:\left(\pi−\theta−{C}+\theta\right)} \\ $$$$\frac{{BQ}}{\mathrm{sin}\:\left({C}−\theta\right)}=\frac{{CQ}}{\mathrm{sin}\:\theta}=\frac{{a}}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{BQ}=\frac{\mathrm{sin}\:\left({C}−\theta\right)}{\mathrm{sin}\:{C}}×{a} \\ $$$$\Rightarrow{CQ}=\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:{C}}×{a} \\ $$$${similarly} \\ $$$$\Rightarrow{BP}=\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:{B}}×{c} \\ $$$$\Rightarrow{a}'={PQ}={BQ}−{BP}=\frac{\mathrm{sin}\:\left({C}−\theta\right)}{\mathrm{sin}\:{C}}×{a}−\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:{B}}×{c} \\ $$$$\Rightarrow{a}'=\frac{{c}\lambda\:\mathrm{cos}\:\theta−\mathrm{cos}\:{C}\:\mathrm{sin}\:\theta}{{c}\lambda}×{a}−\frac{\mathrm{sin}\:\theta}{{b}\lambda}×{c} \\ $$$$\Rightarrow{a}'={a}\:\mathrm{cos}\:\theta−\frac{\left({ab}\:\mathrm{cos}\:{C}+{c}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{{bc}\lambda} \\ $$$$\Rightarrow{a}'={a}\:\mathrm{cos}\:\theta−\frac{\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}}+{c}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{{bc}\lambda} \\ $$$$\Rightarrow{a}'={a}\:\mathrm{cos}\:\theta−\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{\mathrm{2}{bc}\lambda} \\ $$$$\Rightarrow{a}'=\left[\mathrm{cos}\:\theta−\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{\mathrm{4}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}\right]{a}={k}\:{a} \\ $$$${similarly} \\ $$$$\Rightarrow{b}'={k}\:{b} \\ $$$$\Rightarrow{c}'={k}\:{c} \\ $$$$\Rightarrow{r}={k}\:{r}_{\Delta{ABC}} ={k}\:\frac{\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}{{s}} \\ $$$$\Rightarrow{r}=\left[\mathrm{cos}\:\theta−\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{\mathrm{4}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}\right]×\sqrt{\frac{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}{{s}}} \\ $$
Commented by ajfour last updated on 27/Feb/18
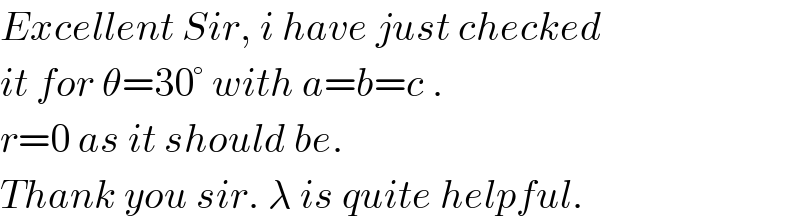
$${Excellent}\:{Sir},\:{i}\:{have}\:{just}\:{checked} \\ $$$${it}\:{for}\:\theta=\mathrm{30}°\:{with}\:{a}={b}={c}\:. \\ $$$${r}=\mathrm{0}\:{as}\:{it}\:{should}\:{be}. \\ $$$${Thank}\:{you}\:{sir}.\:\lambda\:{is}\:{quite}\:{helpful}. \\ $$
