Question Number 161945 by Ahmed777hamouda last updated on 24/Dec/21
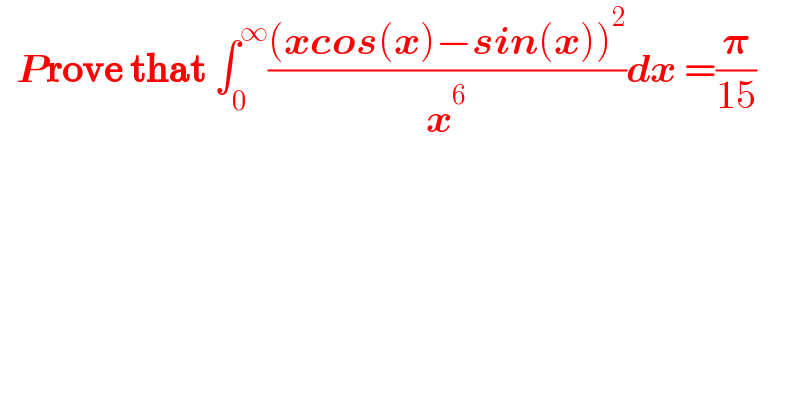
$$\:\:\boldsymbol{{P}\mathrm{rove}}\:\boldsymbol{\mathrm{that}}\:\int_{\mathrm{0}} ^{\infty} \frac{\left(\boldsymbol{{xcos}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\right)^{\mathrm{2}} }{\boldsymbol{{x}}^{\mathrm{6}} }\boldsymbol{{dx}}\:=\frac{\boldsymbol{\pi}}{\mathrm{15}} \\ $$
Answered by Ar Brandon last updated on 24/Dec/21
![I=∫_0 ^∞ (((xcosx−sinx)^2 )/x^6 )dx=∫_0 ^∞ (((cos^2 x)/x^4 )−((sin2x)/x^5 )+((sin^2 x)/x^6 ))dx =[−((cos^2 x)/(3x^3 ))]_0 ^∞ −(1/3)∫((sin2x)/x^3 )dx−16∫_0 ^∞ ((sinu)/u^5 )du−[((sin^2 x)/(5x^5 ))]_0 ^∞ +(1/5)∫_0 ^∞ ((sin2x)/x^5 )dx =−(4/3)∫_0 ^∞ ((sint)/t^3 )dt−16∫_0 ^∞ ((sinu)/u^5 )du+((16)/5)∫_0 ^∞ ((sint)/t^5 )dt =−(4/3)∙(π/(2Γ(3)sin(((3π)/2))))−((64)/5)∙(π/(2Γ(5)sin(((5π)/2))))=(π/3)−((4π)/(15))=(π/(15))](https://www.tinkutara.com/question/Q161949.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \frac{\left({x}\mathrm{cos}{x}−\mathrm{sin}{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{6}} }{dx}=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{cos}^{\mathrm{2}} {x}}{{x}^{\mathrm{4}} }−\frac{\mathrm{sin2}{x}}{{x}^{\mathrm{5}} }+\frac{\mathrm{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{6}} }\right){dx} \\ $$$$\:\:\:=\left[−\frac{\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{3}{x}^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{sin2}{x}}{{x}^{\mathrm{3}} }{dx}−\mathrm{16}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}^{\mathrm{5}} }{du}−\left[\frac{\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{5}{x}^{\mathrm{5}} }\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin2}{x}}{{x}^{\mathrm{5}} }{dx} \\ $$$$\:\:\:=−\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{t}^{\mathrm{3}} }{dt}−\mathrm{16}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}^{\mathrm{5}} }{du}+\frac{\mathrm{16}}{\mathrm{5}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{t}^{\mathrm{5}} }{dt} \\ $$$$\:\:\:=−\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\pi}{\mathrm{2}\Gamma\left(\mathrm{3}\right)\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)}−\frac{\mathrm{64}}{\mathrm{5}}\centerdot\frac{\pi}{\mathrm{2}\Gamma\left(\mathrm{5}\right)\mathrm{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{2}}\right)}=\frac{\pi}{\mathrm{3}}−\frac{\mathrm{4}\pi}{\mathrm{15}}=\frac{\pi}{\mathrm{15}} \\ $$
