Question Number 161968 by naka3546 last updated on 24/Dec/21
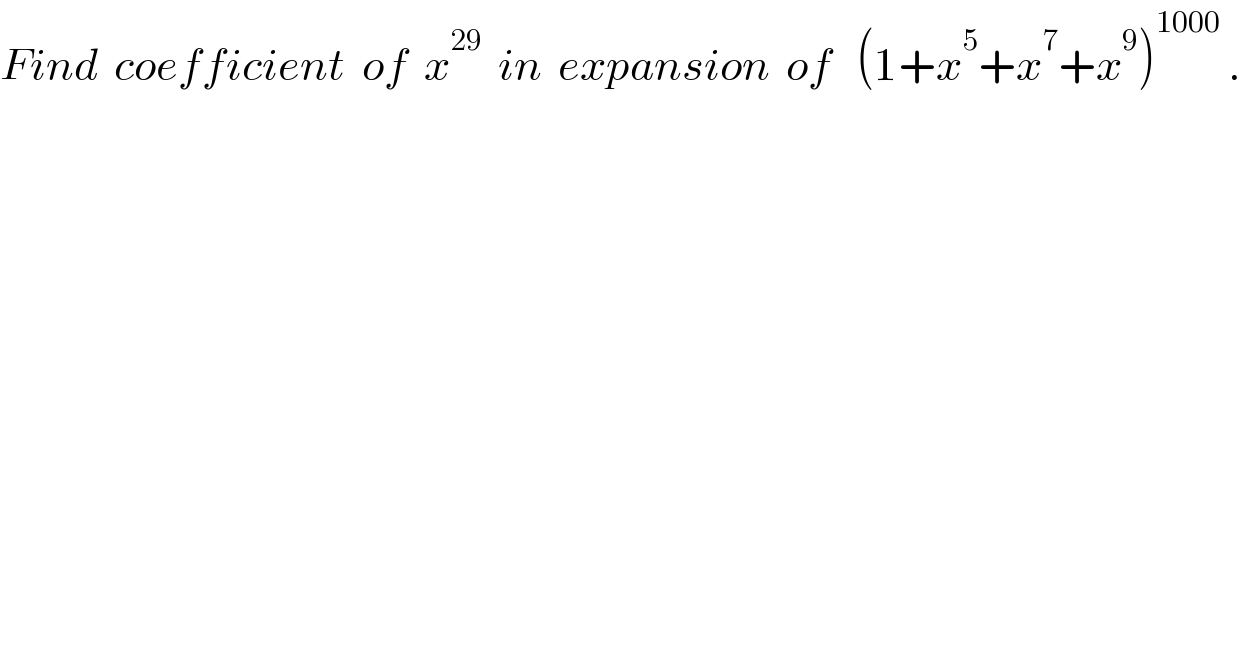
$${Find}\:\:{coefficient}\:\:{of}\:\:{x}^{\mathrm{29}} \:\:{in}\:\:{expansion}\:\:{of}\:\:\:\left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{7}} +{x}^{\mathrm{9}} \right)^{\mathrm{1000}} \:. \\ $$
Answered by mr W last updated on 25/Dec/21
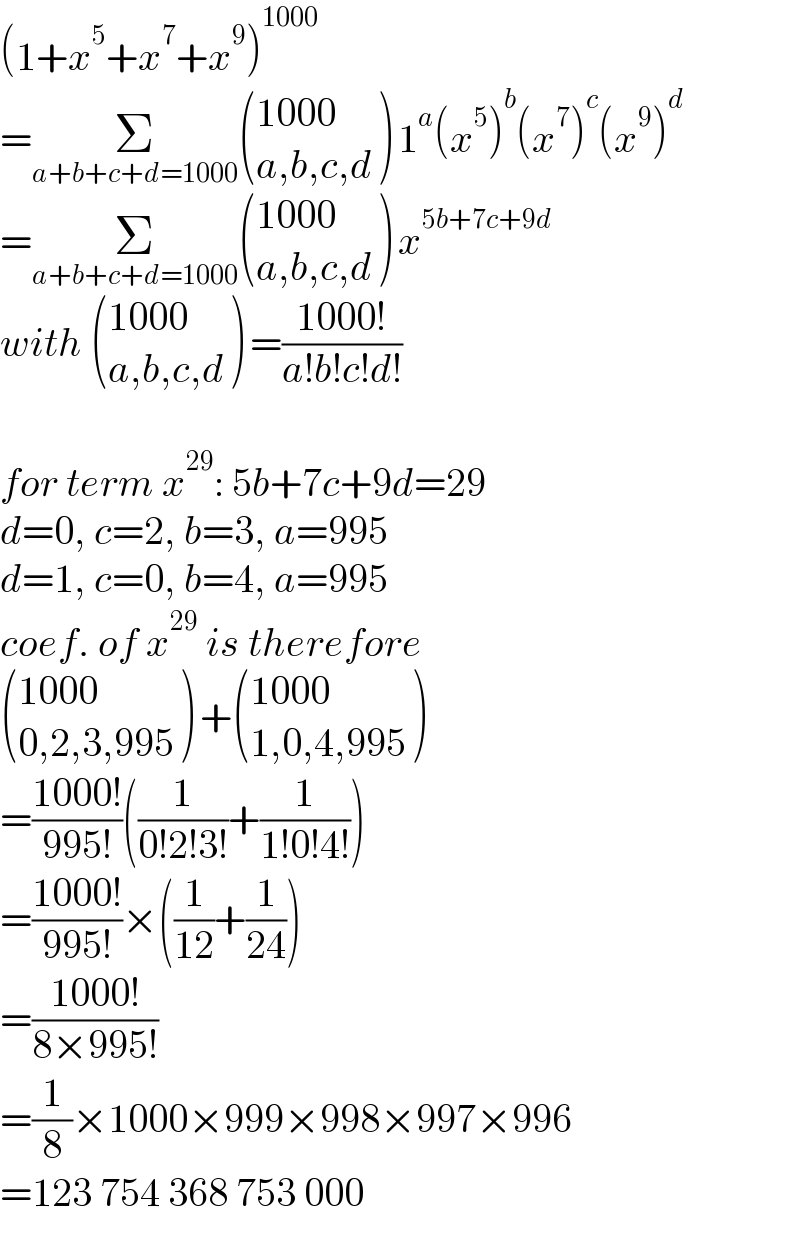
$$\left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{7}} +{x}^{\mathrm{9}} \right)^{\mathrm{1000}} \\ $$$$=\underset{{a}+{b}+{c}+{d}=\mathrm{1000}} {\sum}\begin{pmatrix}{\mathrm{1000}}\\{{a},{b},{c},{d}}\end{pmatrix}\:\mathrm{1}^{{a}} \left({x}^{\mathrm{5}} \right)^{{b}} \left({x}^{\mathrm{7}} \right)^{{c}} \left({x}^{\mathrm{9}} \right)^{{d}} \\ $$$$=\underset{{a}+{b}+{c}+{d}=\mathrm{1000}} {\sum}\begin{pmatrix}{\mathrm{1000}}\\{{a},{b},{c},{d}}\end{pmatrix}\:{x}^{\mathrm{5}{b}+\mathrm{7}{c}+\mathrm{9}{d}} \\ $$$${with}\:\begin{pmatrix}{\mathrm{1000}}\\{{a},{b},{c},{d}}\end{pmatrix}\:=\frac{\mathrm{1000}!}{{a}!{b}!{c}!{d}!} \\ $$$$ \\ $$$${for}\:{term}\:{x}^{\mathrm{29}} :\:\mathrm{5}{b}+\mathrm{7}{c}+\mathrm{9}{d}=\mathrm{29} \\ $$$${d}=\mathrm{0},\:{c}=\mathrm{2},\:{b}=\mathrm{3},\:{a}=\mathrm{995} \\ $$$${d}=\mathrm{1},\:{c}=\mathrm{0},\:{b}=\mathrm{4},\:{a}=\mathrm{995} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{29}} \:{is}\:{therefore} \\ $$$$\begin{pmatrix}{\mathrm{1000}}\\{\mathrm{0},\mathrm{2},\mathrm{3},\mathrm{995}}\end{pmatrix}\:+\begin{pmatrix}{\mathrm{1000}}\\{\mathrm{1},\mathrm{0},\mathrm{4},\mathrm{995}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1000}!}{\mathrm{995}!}\left(\frac{\mathrm{1}}{\mathrm{0}!\mathrm{2}!\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{1}!\mathrm{0}!\mathrm{4}!}\right) \\ $$$$=\frac{\mathrm{1000}!}{\mathrm{995}!}×\left(\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{24}}\right) \\ $$$$=\frac{\mathrm{1000}!}{\mathrm{8}×\mathrm{995}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{1000}×\mathrm{999}×\mathrm{998}×\mathrm{997}×\mathrm{996} \\ $$$$=\mathrm{123}\:\mathrm{754}\:\mathrm{368}\:\mathrm{753}\:\mathrm{000} \\ $$
Commented by naka3546 last updated on 25/Dec/21
$${Thank}\:\:{you},\:\:{sir}. \\ $$
Commented by Tawa11 last updated on 25/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Jamshidbek last updated on 25/Dec/21

$$\mathrm{Which}\:\mathrm{is}\:\mathrm{this}\:\mathrm{theorem}? \\ $$
Commented by mr W last updated on 25/Dec/21
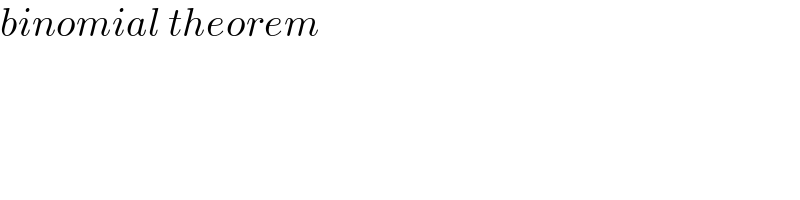
$${binomial}\:{theorem} \\ $$
Commented by mr W last updated on 25/Dec/21

Commented by Jamshidbek last updated on 25/Dec/21

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
