Question Number 31071 by abdo imad last updated on 02/Mar/18
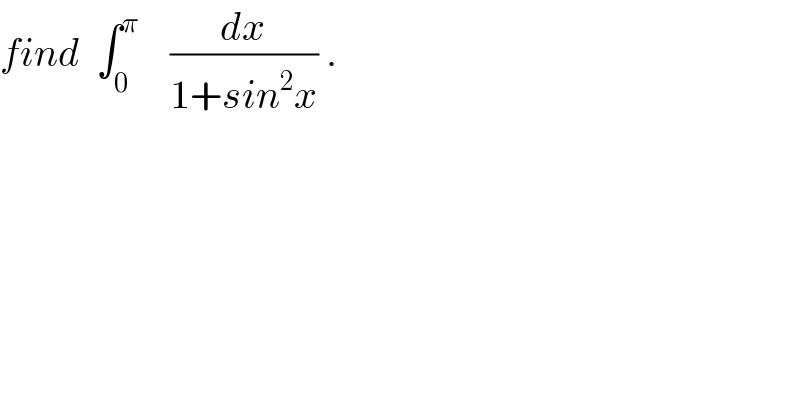
$${find}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}\:. \\ $$
Commented by abdo imad last updated on 03/Mar/18

$${thanks}. \\ $$
Commented by abdo imad last updated on 02/Mar/18

$${let}\:{put}\:{I}=\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}\:\Rightarrow\:{I}=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{\mathrm{1}+\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \\ $$$$=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{\mathrm{2}{dx}}{\mathrm{3}−{cos}\left(\mathrm{2}{x}\right)}\:\:=_{{t}=\mathrm{2}{x}} \:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{{dt}}{\mathrm{3}−{cost}}\:{the}\:{ch}.\:{e}^{{it}} ={z}\:{give} \\ $$$${I}=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{3}\:−\frac{{z}\:+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}}\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2}{dz}}{{iz}\left(\mathrm{6}−\left({z}+{z}^{−\mathrm{1}} \right)\right)} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \frac{−\mathrm{2}{idz}}{\mathrm{6}{z}\:−{z}^{\mathrm{2}} \:−\mathrm{1}}=\:\int_{\mid{z}\mid=\mathrm{1}} \:\frac{\mathrm{2}{idz}}{{z}^{\mathrm{2}} \:−\mathrm{6}{z}+\mathrm{1}}\:{let}\:{put} \\ $$$$\varphi\left({z}\right)=\:\frac{\mathrm{2}{i}}{{z}^{\mathrm{2}} \:−\mathrm{6}{z}\:+\mathrm{1}}\:.{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} \:−\mathrm{6}{z}\:+\mathrm{1}=\mathrm{0}\:\Rightarrow\Delta^{'} =\left(−\mathrm{3}\right)^{\mathrm{2}} \:−\mathrm{1}=\mathrm{8}\:\Rightarrow{z}_{\mathrm{1}} =\mathrm{3}\:+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\:\:\:\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{1}=\mathrm{2}\:+\mathrm{2}\sqrt{\mathrm{2}}\:\:>\mathrm{0}\left({to}\:{eliminate}\right. \\ $$$$\left.{from}\:{residus}\right)\:\mid{z}_{\mathrm{2}} \mid\:−\mathrm{1}=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\:=\mathrm{2}\left(\mathrm{1}−\sqrt{\left.\mathrm{2}\right)}<\mathrm{0}\:\Rightarrow\right. \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:{but} \\ $$$$\varphi\left({z}\right)=\:\frac{\mathrm{2}{i}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\Rightarrow{Res}\left(\varphi,{z}_{\mathrm{2}} \right)=\:\frac{\mathrm{2}{i}}{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\:=\:\frac{\mathrm{2}{i}}{−\mathrm{4}\sqrt{\mathrm{2}}}\:=\frac{−{i}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}=\mathrm{2}{i}\pi.\frac{−{i}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\:\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\:\Rightarrow\:{I}=\:\frac{\pi}{\:\sqrt{\mathrm{2}}}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by Joel578 last updated on 02/Mar/18

$$\mathrm{Nice}\:\mathrm{solution},\:\mathrm{Sir} \\ $$
Answered by Joel578 last updated on 02/Mar/18
![I = ∫_0 ^π ((cosec^2 x )/((1 + sin^2 x)cosec^2 x)) dx = ∫_0 ^π ((cosec^2 x)/(cosec^2 x + 1)) dx = ∫_0 ^π ((cosec^2 x)/(cot^2 x + 2)) dx u = cot x → du = −cosec^2 x dx = −∫ ((cosec^2 x)/(u^2 + 2)) . (du/(cosec^2 x)) = −∫ (du/(u^2 + 2)) u = (√2) tan θ → du = (√2) sec^2 θ dθ I = −(√2)∫ ((sec^2 θ)/(2(tan^2 θ + 1))) dθ = −((√2)/2) ∫ dθ = −((√2)/2)θ + C = −((√2)/2)tan^(−1) ((u/( (√2)))) + C = −((√2)/2)tan^(−1) (((cot x)/( (√2)))) + C I = [−((√2)/2)tan^(−1) (((cot x)/( (√2))))]_0 ^π = (−((√2)/2)tan^(−1) (−∞)) − (−((√2)/2)tan^(−1) (∞)) = ((π(√2))/4) + ((π(√2))/4) = ((π(√2))/2)](https://www.tinkutara.com/question/Q31116.png)
$${I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosec}^{\mathrm{2}} \:{x}\:}{\left(\mathrm{1}\:+\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)\mathrm{cosec}^{\mathrm{2}} \:{x}}\:{dx} \\ $$$$\:\:\:=\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosec}^{\mathrm{2}} \:{x}}{\mathrm{cosec}^{\mathrm{2}} \:{x}\:+\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:=\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosec}^{\mathrm{2}} \:{x}}{\mathrm{cot}^{\mathrm{2}} \:{x}\:+\:\mathrm{2}}\:{dx} \\ $$$$ \\ $$$${u}\:=\:\mathrm{cot}\:{x}\:\:\rightarrow\:\:{du}\:=\:−\mathrm{cosec}^{\mathrm{2}} \:{x}\:{dx} \\ $$$$\:=\:−\int\:\frac{\mathrm{cosec}^{\mathrm{2}} \:{x}}{{u}^{\mathrm{2}} \:+\:\mathrm{2}}\:.\:\frac{{du}}{\mathrm{cosec}^{\mathrm{2}} \:{x}}\:=\:−\int\:\frac{{du}}{{u}^{\mathrm{2}} \:+\:\mathrm{2}} \\ $$$$ \\ $$$${u}\:=\:\sqrt{\mathrm{2}}\:\mathrm{tan}\:\theta\:\:\rightarrow\:\:{du}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sec}^{\mathrm{2}} \:\theta\:{d}\theta \\ $$$${I}\:=\:−\sqrt{\mathrm{2}}\int\:\frac{\mathrm{sec}^{\mathrm{2}} \:\theta}{\mathrm{2}\left(\mathrm{tan}^{\mathrm{2}} \:\theta\:+\:\mathrm{1}\right)}\:{d}\theta\: \\ $$$$\:\:\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int\:{d}\theta \\ $$$$\:\:\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\theta\:+\:{C}\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{u}}{\:\sqrt{\mathrm{2}}}\right)\:+\:{C} \\ $$$$\:\:\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{cot}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:\left[−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{cot}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$\:\:\:=\:\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(−\infty\right)\right)\:−\:\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\infty\right)\right) \\ $$$$\:\:\:=\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:+\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
