Menu Close

find-0-lnx-x-2-a-2-dx-2-find-the-value-of-0-lnx-x-2-a-2-3-

Tinku Tara 0 Comments
Pin




Question Number 31102 by abdo imad last updated on 02/Mar/18
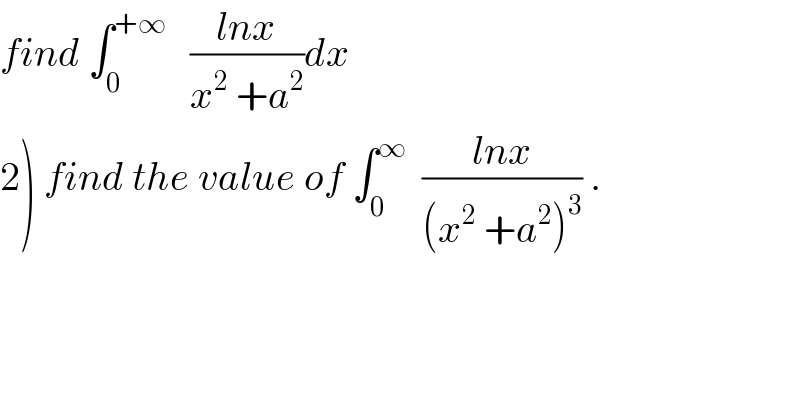
find ∫_0 ^(+∞) ((lnx)/(x^2 +a^2 ))dx 2) find the value of ∫_0 ^∞ ((lnx)/((x^2 +a^2 )^3 )) .
$${find}\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{lnx}}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{3}} }\:. \\ $$
Commented by abdo imad last updated on 05/Mar/18
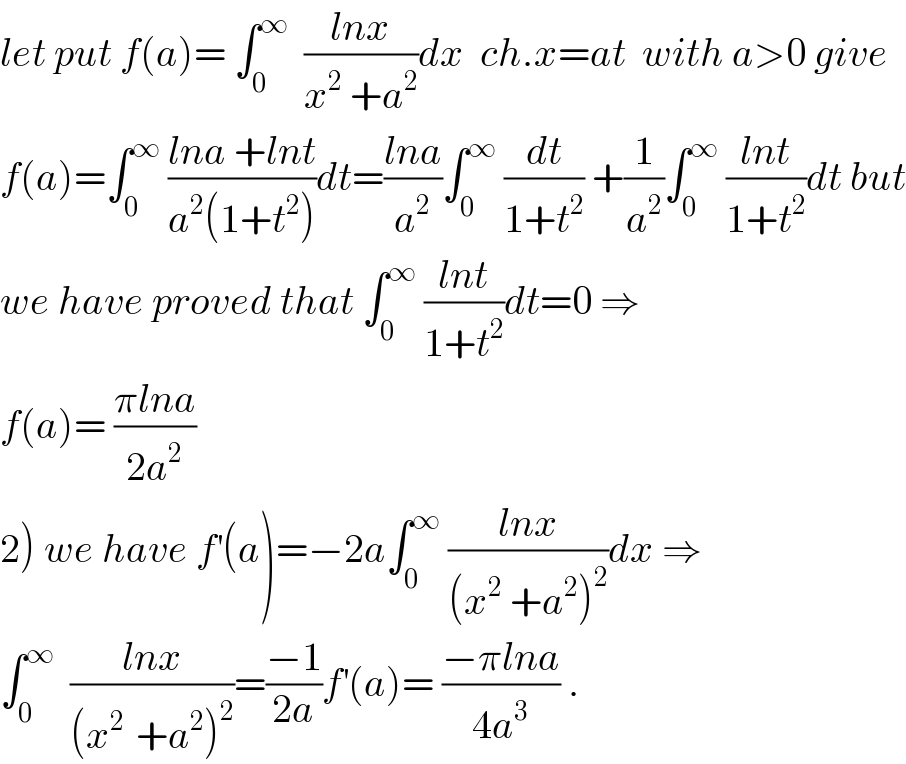
let put f(a)= ∫_0 ^∞ ((lnx)/(x^2 +a^2 ))dx ch.x=at with a>0 give f(a)=∫_0 ^∞ ((lna +lnt)/(a^2 (1+t^2 )))dt=((lna)/a^2 )∫_0 ^∞ (dt/(1+t^2 )) +(1/a^2 )∫_0 ^∞ ((lnt)/(1+t^2 ))dt but we have proved that ∫_0 ^∞ ((lnt)/(1+t^2 ))dt=0 ⇒ f(a)= ((πlna)/(2a^2 )) 2) we have f^′ (a)=−2a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^2 ))dx ⇒ ∫_0 ^∞ ((lnx)/((x^(2 ) +a^2 )^2 ))=((−1)/(2a))f^′ (a)= ((−πlna)/(4a^3 )) .
$${let}\:{put}\:{f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:\:{ch}.{x}={at}\:\:{with}\:{a}>\mathrm{0}\:{give} \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{lna}\:+{lnt}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}=\frac{{lna}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{{lnt}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{but} \\ $$$${we}\:{have}\:{proved}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{lnt}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{0}\:\Rightarrow \\ $$$${f}\left({a}\right)=\:\frac{\pi{lna}}{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({a}\right)=−\mathrm{2}{a}\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}\:} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{−\mathrm{1}}{\mathrm{2}{a}}{f}^{'} \left({a}\right)=\:\frac{−\pi{lna}}{\mathrm{4}{a}^{\mathrm{3}} }\:. \\ $$
Commented by abdo imad last updated on 05/Mar/18
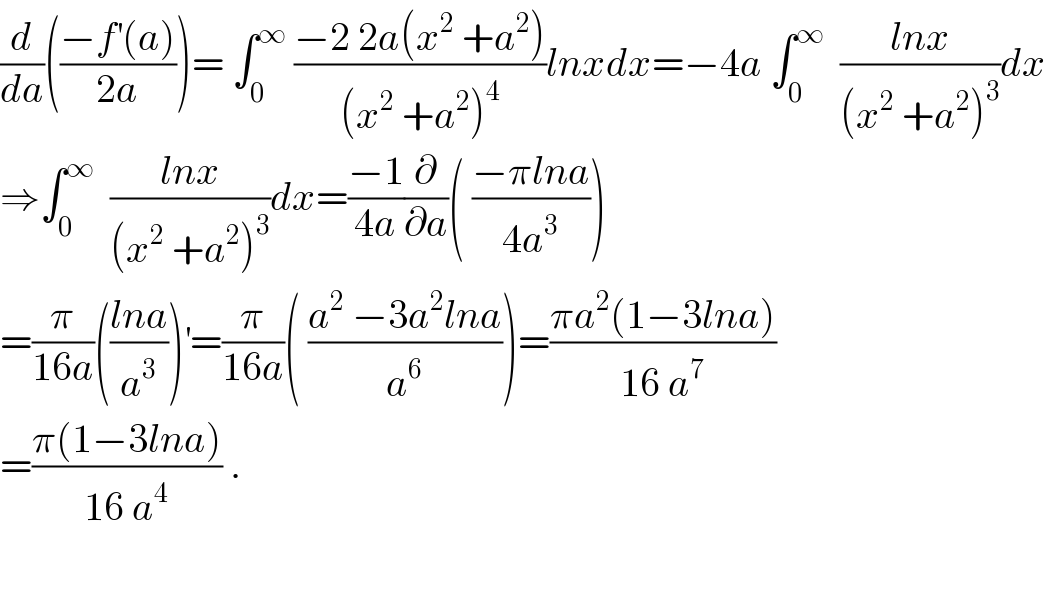
(d/da)(((−f^′ (a))/(2a)))= ∫_0 ^∞ ((−2 2a(x^2 +a^2 ))/((x^2 +a^2 )^4 ))lnxdx=−4a ∫_0 ^∞ ((lnx)/((x^2 +a^2 )^3 ))dx ⇒∫_0 ^∞ ((lnx)/((x^2 +a^2 )^3 ))dx=((−1)/(4a))(∂/∂a)( ((−πlna)/(4a^3 ))) =(π/(16a))(((lna)/a^3 ))^′ =(π/(16a))( ((a^2 −3a^2 lna)/a^6 ))=((πa^2 (1−3lna))/(16 a^7 )) =((π(1−3lna))/(16 a^4 )) .
$$\frac{{d}}{{da}}\left(\frac{−{f}^{'} \left({a}\right)}{\mathrm{2}{a}}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\frac{−\mathrm{2}\:\mathrm{2}{a}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{4}} }{lnxdx}=−\mathrm{4}{a}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx}=\frac{−\mathrm{1}}{\mathrm{4}{a}}\frac{\partial}{\partial{a}}\left(\:\frac{−\pi{lna}}{\mathrm{4}{a}^{\mathrm{3}} }\right) \\ $$$$=\frac{\pi}{\mathrm{16}{a}}\left(\frac{{lna}}{{a}^{\mathrm{3}} }\right)^{'} =\frac{\pi}{\mathrm{16}{a}}\left(\:\frac{{a}^{\mathrm{2}} \:−\mathrm{3}{a}^{\mathrm{2}} {lna}}{{a}^{\mathrm{6}} }\right)=\frac{\pi{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{lna}\right)}{\mathrm{16}\:{a}^{\mathrm{7}} } \\ $$$$=\frac{\pi\left(\mathrm{1}−\mathrm{3}{lna}\right)}{\mathrm{16}\:{a}^{\mathrm{4}} }\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *