Question Number 133989 by Mamifere last updated on 26/Feb/21
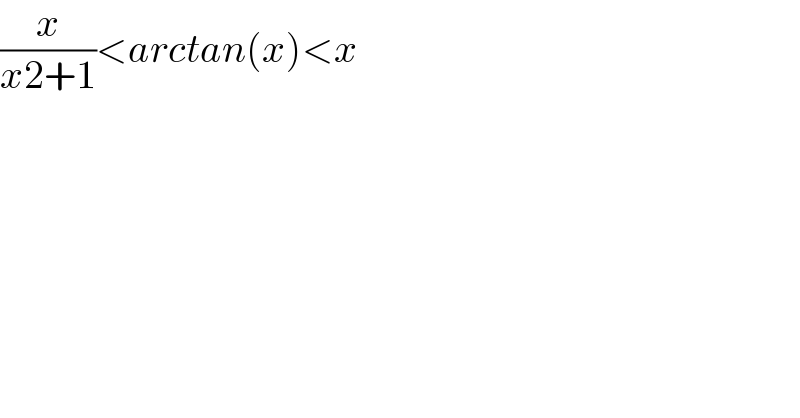
$$\frac{{x}}{{x}\mathrm{2}+\mathrm{1}}<{arctan}\left({x}\right)<{x} \\ $$$$ \\ $$
Answered by Ñï= last updated on 26/Feb/21
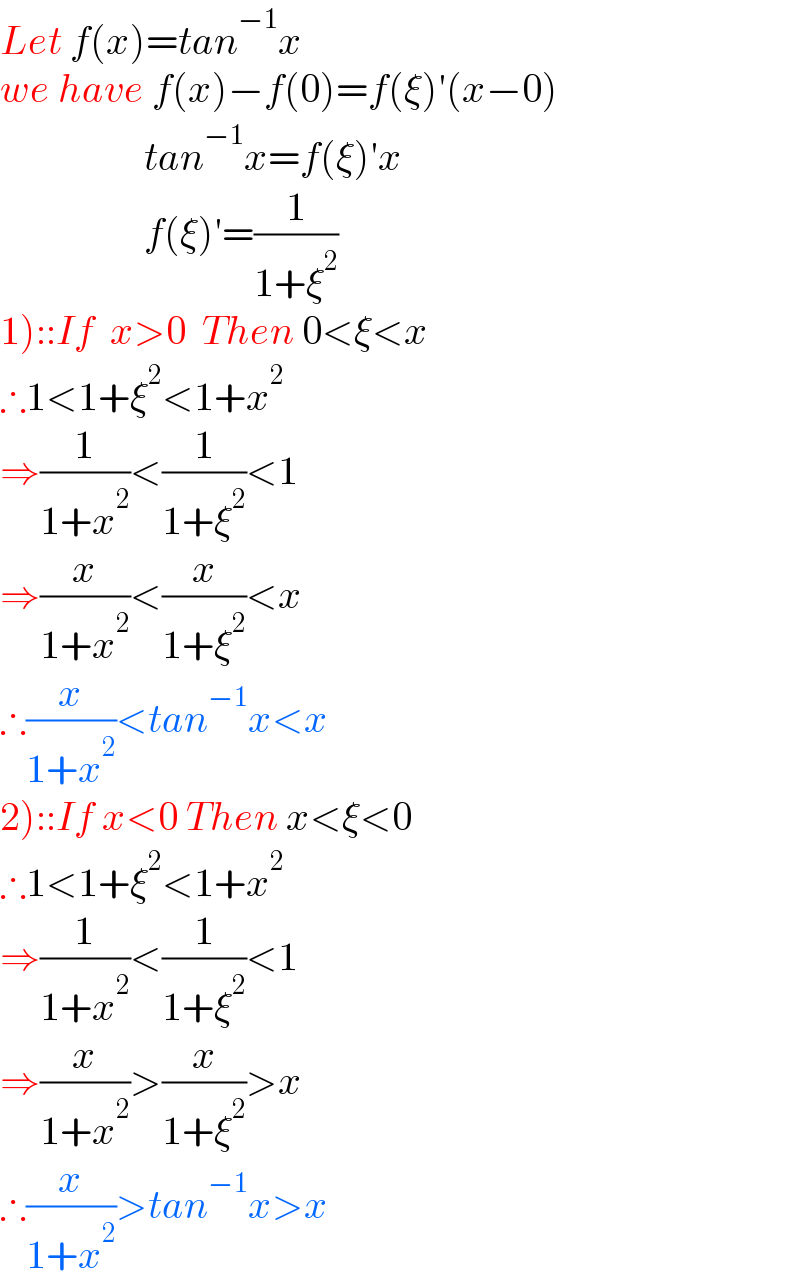
$${Let}\:{f}\left({x}\right)={tan}^{−\mathrm{1}} {x} \\ $$$${we}\:{have}\:{f}\left({x}\right)−{f}\left(\mathrm{0}\right)={f}\left(\xi\right)'\left({x}−\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tan}^{−\mathrm{1}} {x}={f}\left(\xi\right)'{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\xi\right)'=\frac{\mathrm{1}}{\mathrm{1}+\xi^{\mathrm{2}} } \\ $$$$\left.\mathrm{1}\right)::{If}\:\:{x}>\mathrm{0}\:\:{Then}\:\mathrm{0}<\xi<{x} \\ $$$$\therefore\mathrm{1}<\mathrm{1}+\xi^{\mathrm{2}} <\mathrm{1}+{x}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }<\frac{\mathrm{1}}{\mathrm{1}+\xi^{\mathrm{2}} }<\mathrm{1} \\ $$$$\Rightarrow\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }<\frac{{x}}{\mathrm{1}+\xi^{\mathrm{2}} }<{x} \\ $$$$\therefore\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }<{tan}^{−\mathrm{1}} {x}<{x} \\ $$$$\left.\mathrm{2}\right)::{If}\:{x}<\mathrm{0}\:{Then}\:{x}<\xi<\mathrm{0} \\ $$$$\therefore\mathrm{1}<\mathrm{1}+\xi^{\mathrm{2}} <\mathrm{1}+{x}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }<\frac{\mathrm{1}}{\mathrm{1}+\xi^{\mathrm{2}} }<\mathrm{1} \\ $$$$\Rightarrow\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }>\frac{{x}}{\mathrm{1}+\xi^{\mathrm{2}} }>{x} \\ $$$$\therefore\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }>{tan}^{−\mathrm{1}} {x}>{x} \\ $$
