Question Number 96652 by bobhans last updated on 03/Jun/20
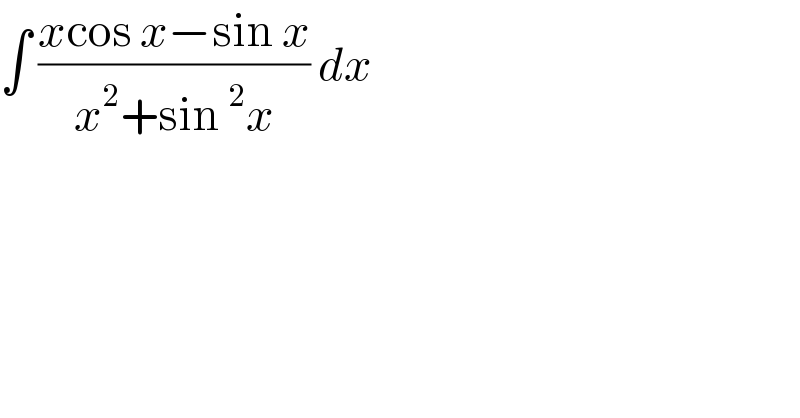
$$\int\:\frac{{x}\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$
Answered by bemath last updated on 03/Jun/20
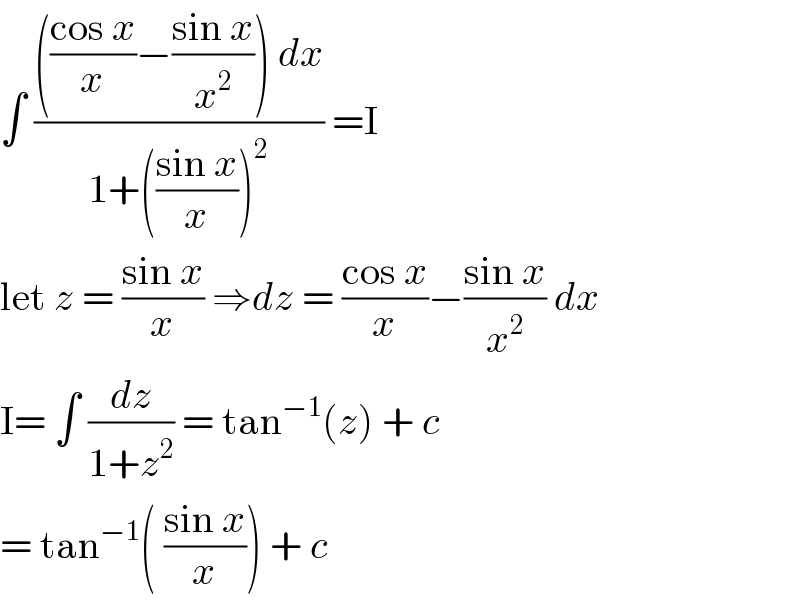
$$\int\:\frac{\left(\frac{\mathrm{cos}\:{x}}{{x}}−\frac{\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} }\right)\:{dx}}{\mathrm{1}+\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} }\:=\mathrm{I} \\ $$$$\mathrm{let}\:{z}\:=\:\frac{\mathrm{sin}\:{x}}{{x}}\:\Rightarrow{dz}\:=\:\frac{\mathrm{cos}\:{x}}{{x}}−\frac{\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} }\:{dx}\: \\ $$$$\mathrm{I}=\:\int\:\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} }\:=\:\mathrm{tan}^{−\mathrm{1}} \left({z}\right)\:+\:{c}\: \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\:\frac{\mathrm{sin}\:{x}}{{x}}\right)\:+\:{c} \\ $$
