Question Number 133997 by rs4089 last updated on 26/Feb/21
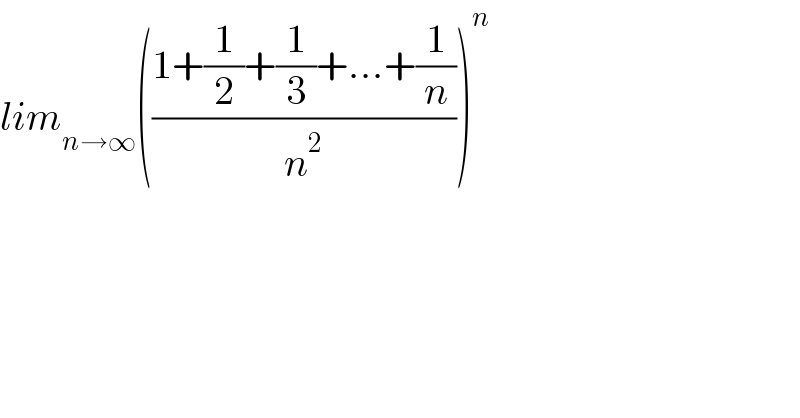
$${lim}_{{n}\rightarrow\infty} \left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{{n}}}{{n}^{\mathrm{2}} }\right)^{{n}} \\ $$
Answered by mathmax by abdo last updated on 27/Feb/21
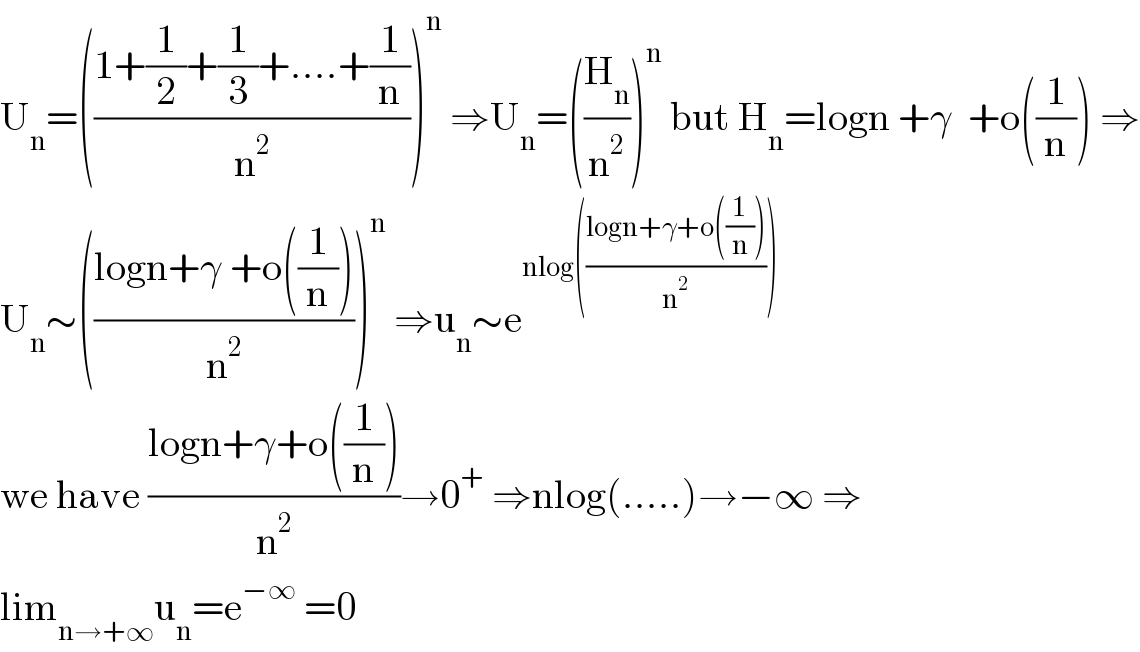
$$\mathrm{U}_{\mathrm{n}} =\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+….+\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\Rightarrow\mathrm{U}_{\mathrm{n}} =\left(\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\mathrm{but}\:\mathrm{H}_{\mathrm{n}} =\mathrm{logn}\:+\gamma\:\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\:\Rightarrow \\ $$$$\mathrm{U}_{\mathrm{n}} \sim\left(\frac{\mathrm{logn}+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} \sim\mathrm{e}^{\mathrm{nlog}\left(\frac{\mathrm{logn}+\gamma+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{logn}+\gamma+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\rightarrow\mathrm{0}^{+} \:\Rightarrow\mathrm{nlog}\left(…..\right)\rightarrow−\infty\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{e}^{−\infty} \:=\mathrm{0} \\ $$
