Question Number 96780 by mr W last updated on 04/Jun/20

Commented by mr W last updated on 04/Jun/20
$${nobody}\:{understands}? \\ $$
Commented by mathmax by abdo last updated on 04/Jun/20
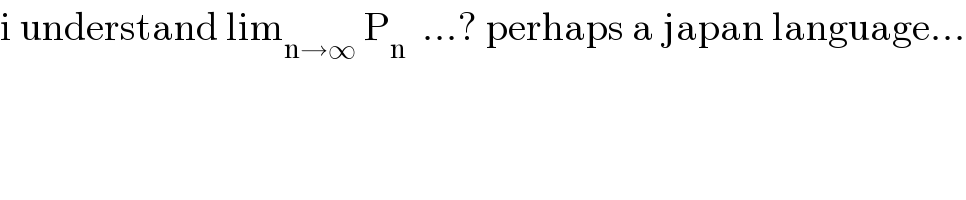
$$\mathrm{i}\:\mathrm{understand}\:\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \:\mathrm{P}_{\mathrm{n}} \:\:…?\:\mathrm{perhaps}\:\mathrm{a}\:\mathrm{japan}\:\mathrm{language}… \\ $$
Commented by mr W last updated on 05/Jun/20

$${After}\:{using}\:{translation}\:{app}\:{I}\:{think} \\ $$$${the}\:{question}\:{is}: \\ $$$${In}\:{a}\:{box}\:{there}\:{are}\:\mathrm{3}{n}\:{write}\:{balls}\:{and} \\ $$$$\mathrm{2}{n}\:{red}\:{balls}.\:{Three}\:{balls}\:{are}\:{taken}\:{from} \\ $$$${the}\:{box}.\:{If}\:{P}_{{n}} \:{is}\:{the}\:{probability}\:{that} \\ $$$$\mathrm{2}\:{white}\:{balls}\:{and}\:\mathrm{1}\:{red}\:{ball}\:{are}\:{taken}, \\ $$$${find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{P}_{{n}} =?. \\ $$
Commented by john santu last updated on 05/Jun/20
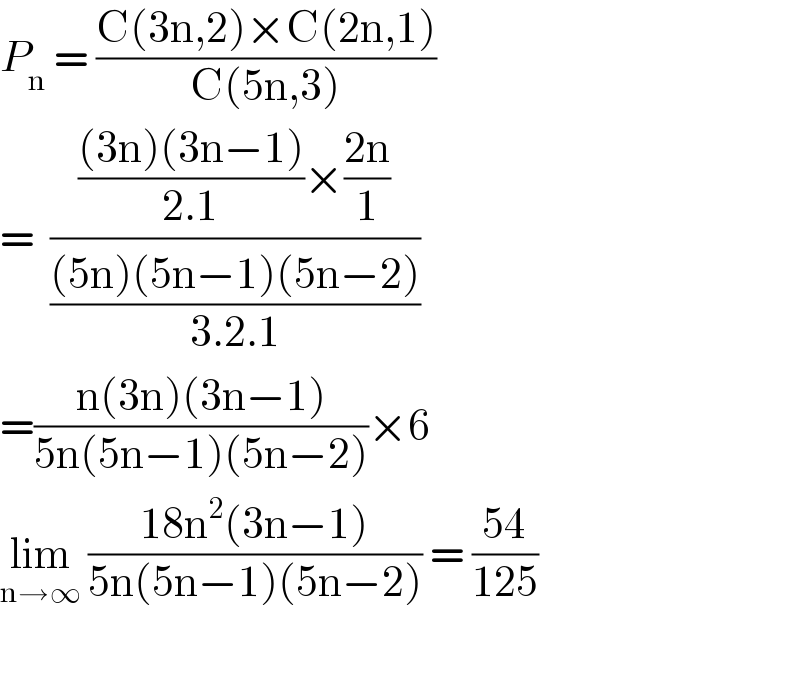
$${P}_{\mathrm{n}} \:=\:\frac{\mathrm{C}\left(\mathrm{3n},\mathrm{2}\right)×\mathrm{C}\left(\mathrm{2n},\mathrm{1}\right)}{\mathrm{C}\left(\mathrm{5n},\mathrm{3}\right)} \\ $$$$=\:\:\frac{\frac{\left(\mathrm{3n}\right)\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}.\mathrm{1}}×\frac{\mathrm{2n}}{\mathrm{1}}}{\frac{\left(\mathrm{5n}\right)\left(\mathrm{5n}−\mathrm{1}\right)\left(\mathrm{5n}−\mathrm{2}\right)}{\mathrm{3}.\mathrm{2}.\mathrm{1}}} \\ $$$$=\frac{\mathrm{n}\left(\mathrm{3n}\right)\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{5n}\left(\mathrm{5n}−\mathrm{1}\right)\left(\mathrm{5n}−\mathrm{2}\right)}×\mathrm{6} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{18n}^{\mathrm{2}} \left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{5n}\left(\mathrm{5n}−\mathrm{1}\right)\left(\mathrm{5n}−\mathrm{2}\right)}\:=\:\frac{\mathrm{54}}{\mathrm{125}} \\ $$$$ \\ $$
Commented by mr W last updated on 05/Jun/20

$${correct},\:{thanks}! \\ $$
