Question Number 162513 by Lordose last updated on 30/Dec/21
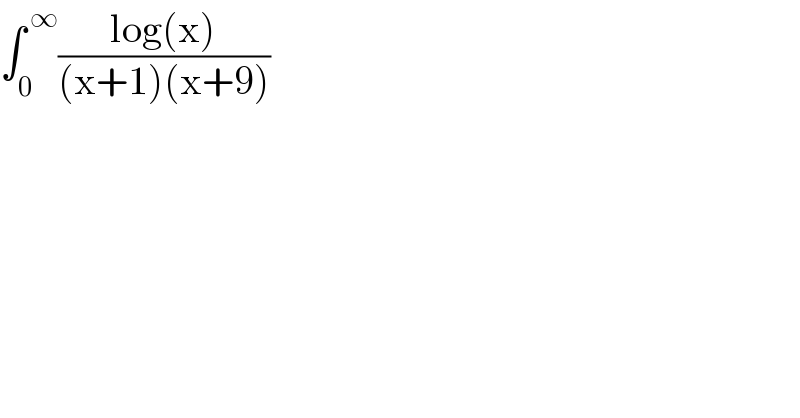
$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{log}\left(\mathrm{x}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{9}\right)} \\ $$
Answered by abdullahoudou last updated on 30/Dec/21

$${x}−>\frac{\mathrm{9}}{{x}} \\ $$
Answered by Lordose last updated on 30/Dec/21
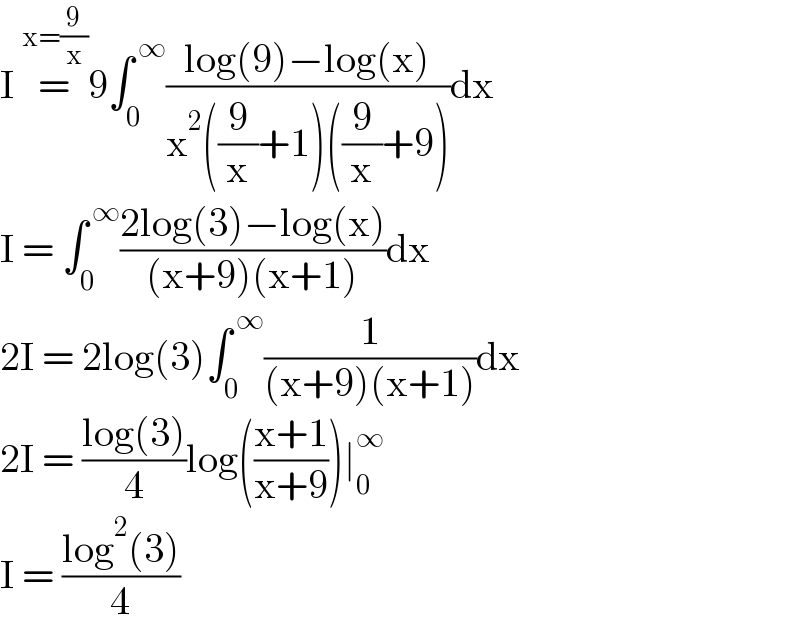
$$\mathrm{I}\:\overset{\mathrm{x}=\frac{\mathrm{9}}{\mathrm{x}}} {=}\mathrm{9}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{log}\left(\mathrm{9}\right)−\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{9}}{\mathrm{x}}+\mathrm{1}\right)\left(\frac{\mathrm{9}}{\mathrm{x}}+\mathrm{9}\right)}\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2log}\left(\mathrm{3}\right)−\mathrm{log}\left(\mathrm{x}\right)}{\left(\mathrm{x}+\mathrm{9}\right)\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{2I}\:=\:\mathrm{2log}\left(\mathrm{3}\right)\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{9}\right)\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{2I}\:=\:\frac{\mathrm{log}\left(\mathrm{3}\right)}{\mathrm{4}}\mathrm{log}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}+\mathrm{9}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{3}\right)}{\mathrm{4}} \\ $$
