Question Number 31476 by NECx last updated on 09/Mar/18

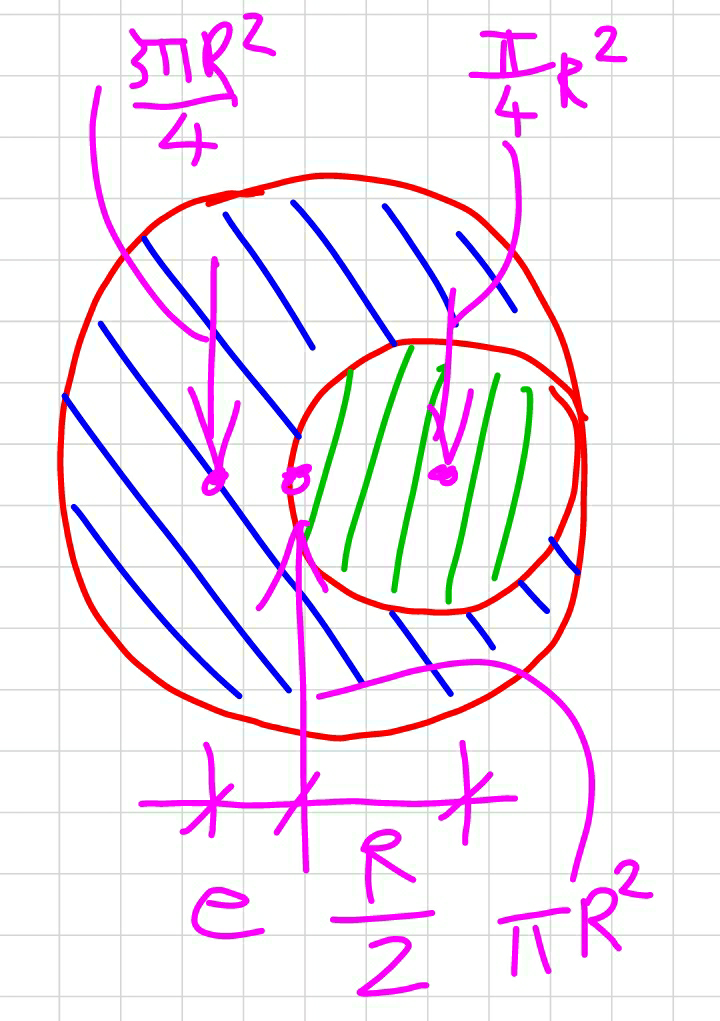
$${From}\:{a}\:{circular}\:{disc}\:{of}\:{radius}\:{R} \\ $$$${a}\:{circular}\:{hole}\:{of}\:{radius}\:{R}/\mathrm{2}\:{is} \\ $$$${cut}\:{out}.{The}\:{centre}\:{of}\:{the}\:{circular} \\ $$$${hole}\:{is}\:{at}\:{R}/\mathrm{2}\:{from}\:{the}\:{centre}\:{of} \\ $$$${the}\:{original}\:{disc}.{Locate}\:{the}\:{centre} \\ $$$${of}\:{gravity}\:{of}\:{the}\:{resulting}\:{flat} \\ $$$${body}. \\ $$$$ \\ $$$${please}\:{help}\:{me}\:{as}\:{fast}\:{as}\:{possible}. \\ $$$${Thanks}! \\ $$
Answered by mrW2 last updated on 09/Mar/18
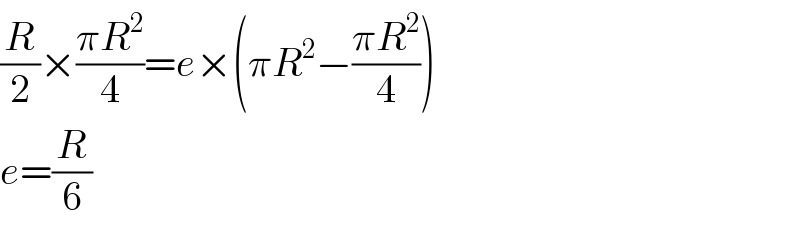
$$\frac{{R}}{\mathrm{2}}×\frac{\pi{R}^{\mathrm{2}} }{\mathrm{4}}={e}×\left(\pi{R}^{\mathrm{2}} −\frac{\pi{R}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${e}=\frac{{R}}{\mathrm{6}} \\ $$
Commented by NECx last updated on 09/Mar/18

$${please}\:{can}\:{you}\:{explain} \\ $$$$ \\ $$
Commented by mrW2 last updated on 09/Mar/18