Question Number 97045 by john santu last updated on 06/Jun/20

$$\mathrm{a}\:\mathrm{committee}\:\mathrm{consisting}\:\mathrm{of} \\ $$$$\mathrm{5}\:\mathrm{men}\:\&\:\mathrm{4}\:\mathrm{women}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\: \\ $$$$\mathrm{chosen}\:\mathrm{from}\:\mathrm{8}\:\mathrm{men}\:\&\:\mathrm{4}\:\mathrm{women}. \\ $$$$\mathrm{If}\:\mathrm{one}\:\mathrm{man}\:\&\:\mathrm{one}\:\mathrm{woman}\:\mathrm{are}\:\mathrm{husband}\: \\ $$$$\&\:\mathrm{wife}\:,\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\: \\ $$$$\mathrm{the}\:\mathrm{committee}\:\mathrm{be}\:\mathrm{chosen}\:\mathrm{if} \\ $$$$\mathrm{only}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{husband}\:\&\:\mathrm{wife} \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{chosen}\:? \\ $$
Commented by bemath last updated on 06/Jun/20
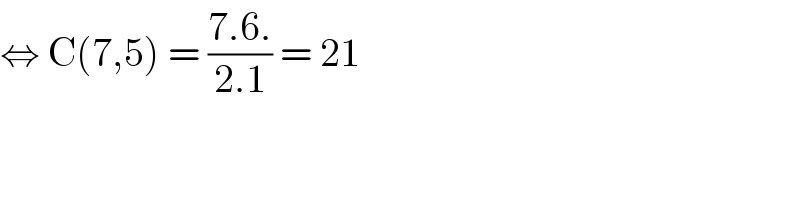
$$\Leftrightarrow\:\mathrm{C}\left(\mathrm{7},\mathrm{5}\right)\:=\:\frac{\mathrm{7}.\mathrm{6}.}{\mathrm{2}.\mathrm{1}}\:=\:\mathrm{21} \\ $$
Commented by mr W last updated on 06/Jun/20

$${since}\:{there}\:{are}\:{only}\:\mathrm{4}\:{women}\:{and} \\ $$$$\mathrm{4}\:{women}\:{must}\:{be}\:{chosen},\:{so}\:{all} \\ $$$${women}\:{must}\:{be}\:{chosen}\:{and}\:{the}\:{wife} \\ $$$${is}\:{always}\:{chosen}\:{and}\:{the}\:{husband} \\ $$$${can}\:{never}\:{be}\:{chosen}.\:{so}\:{the}\:{question} \\ $$$${is}\:{in}\:{how}\:{many}\:{ways}\:{can}\:\mathrm{5}\:{men}\:{be} \\ $$$${chosen}\:{from}\:{the}\:{other}\:\mathrm{7}\:{men},\:{the} \\ $$$${answer}\:{is}\:{C}_{\mathrm{5}} ^{\mathrm{7}} =\mathrm{21}. \\ $$
Commented by bemath last updated on 06/Jun/20
$$\mathrm{oo}\:\mathrm{sorry}.\:\mathrm{i}\:\mathrm{misread}\:\mathrm{the}\:\mathrm{question}\: \\ $$
Commented by john santu last updated on 06/Jun/20
$$\mathrm{yes}.\:\mathrm{right}.\:\mathrm{thank}\:\mathrm{you} \\ $$
