Question Number 31529 by abdo imad last updated on 09/Mar/18
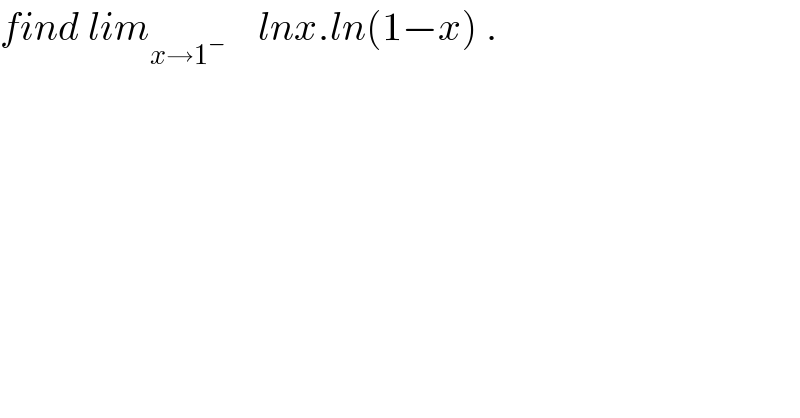
$${find}\:{lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:\:\:{lnx}.{ln}\left(\mathrm{1}−{x}\right)\:. \\ $$
Commented by abdo imad last updated on 11/Mar/18
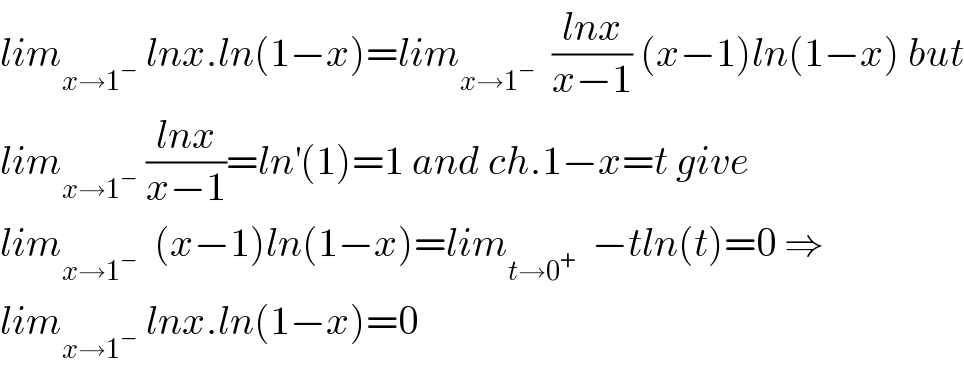
$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:{lnx}.{ln}\left(\mathrm{1}−{x}\right)={lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:\frac{{lnx}}{{x}−\mathrm{1}}\:\left({x}−\mathrm{1}\right){ln}\left(\mathrm{1}−{x}\right)\:{but} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\frac{{lnx}}{{x}−\mathrm{1}}={ln}^{'} \left(\mathrm{1}\right)=\mathrm{1}\:{and}\:{ch}.\mathrm{1}−{x}={t}\:{give} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:\left({x}−\mathrm{1}\right){ln}\left(\mathrm{1}−{x}\right)={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:−{tln}\left({t}\right)=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:{lnx}.{ln}\left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$
