Question Number 2970 by Syaka last updated on 01/Dec/15
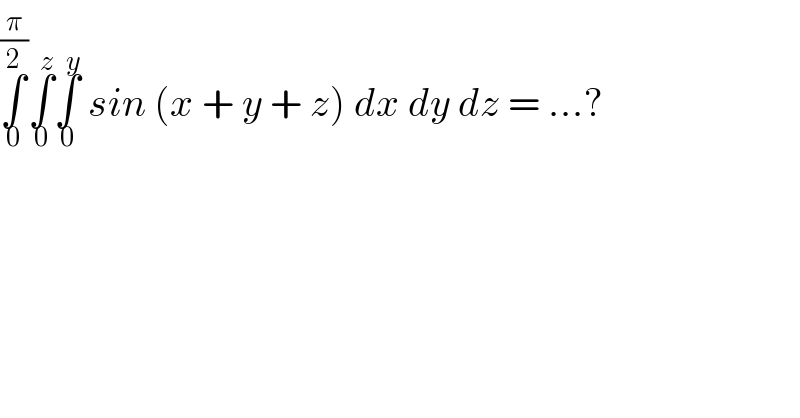
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\underset{\mathrm{0}} {\overset{{z}} {\int}}\underset{\mathrm{0}} {\overset{{y}} {\int}}\:{sin}\:\left({x}\:+\:{y}\:+\:{z}\right)\:{dx}\:{dy}\:{dz}\:=\:…? \\ $$
Answered by Yozzi last updated on 02/Dec/15
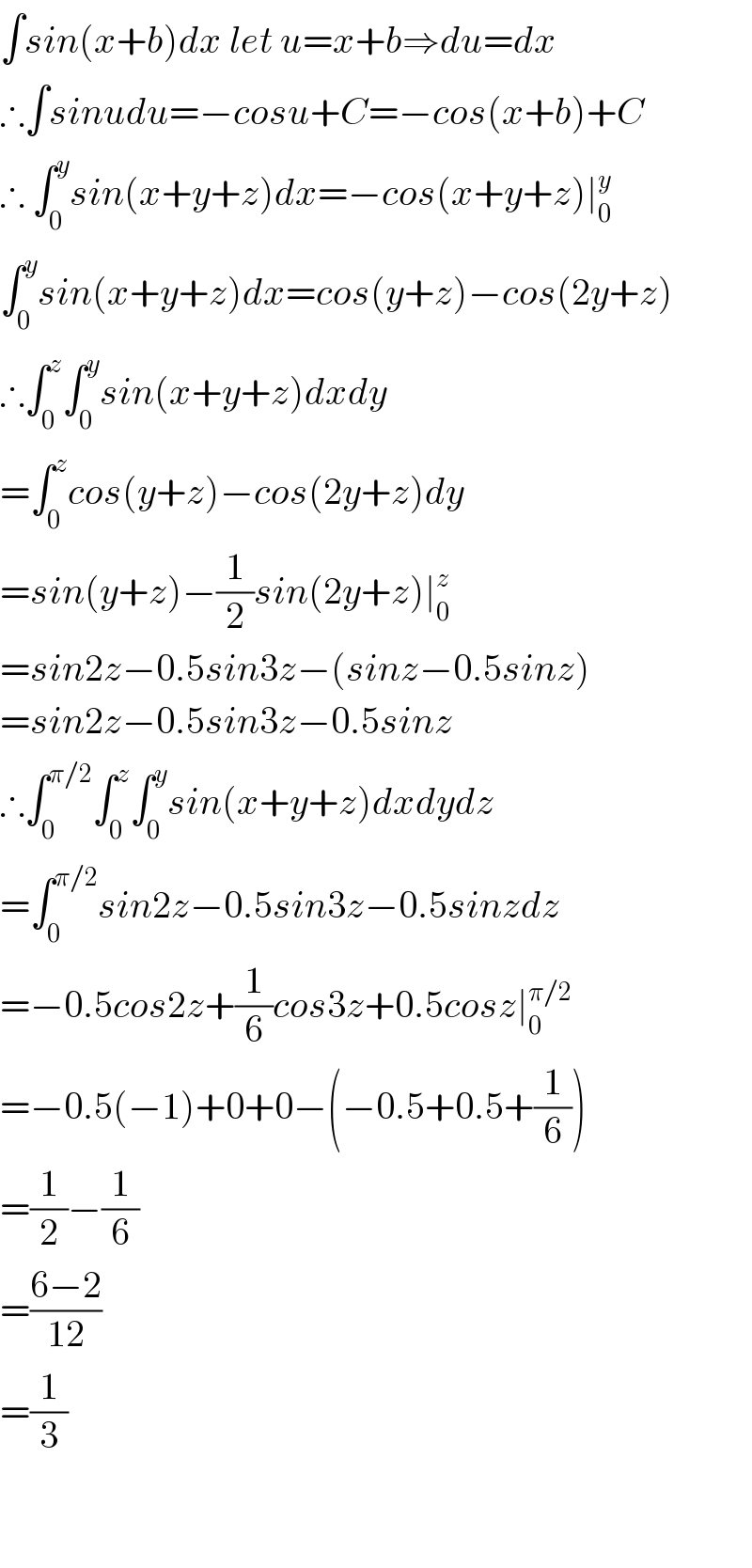
$$\int{sin}\left({x}+{b}\right){dx}\:{let}\:{u}={x}+{b}\Rightarrow{du}={dx} \\ $$$$\therefore\int{sinudu}=−{cosu}+{C}=−{cos}\left({x}+{b}\right)+{C} \\ $$$$\therefore\:\int_{\mathrm{0}} ^{{y}} {sin}\left({x}+{y}+{z}\right){dx}=−{cos}\left({x}+{y}+{z}\right)\mid_{\mathrm{0}} ^{{y}} \\ $$$$\int_{\mathrm{0}} ^{{y}} {sin}\left({x}+{y}+{z}\right){dx}={cos}\left({y}+{z}\right)−{cos}\left(\mathrm{2}{y}+{z}\right) \\ $$$$\therefore\int_{\mathrm{0}} ^{{z}} \int_{\mathrm{0}} ^{{y}} {sin}\left({x}+{y}+{z}\right){dxdy} \\ $$$$=\int_{\mathrm{0}} ^{{z}} {cos}\left({y}+{z}\right)−{cos}\left(\mathrm{2}{y}+{z}\right){dy} \\ $$$$={sin}\left({y}+{z}\right)−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{y}+{z}\right)\mid_{\mathrm{0}} ^{{z}} \\ $$$$={sin}\mathrm{2}{z}−\mathrm{0}.\mathrm{5}{sin}\mathrm{3}{z}−\left({sinz}−\mathrm{0}.\mathrm{5}{sinz}\right) \\ $$$$={sin}\mathrm{2}{z}−\mathrm{0}.\mathrm{5}{sin}\mathrm{3}{z}−\mathrm{0}.\mathrm{5}{sinz} \\ $$$$\therefore\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \int_{\mathrm{0}} ^{{z}} \int_{\mathrm{0}} ^{{y}} {sin}\left({x}+{y}+{z}\right){dxdydz} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}\mathrm{2}{z}−\mathrm{0}.\mathrm{5}{sin}\mathrm{3}{z}−\mathrm{0}.\mathrm{5}{sinzdz} \\ $$$$=−\mathrm{0}.\mathrm{5}{cos}\mathrm{2}{z}+\frac{\mathrm{1}}{\mathrm{6}}{cos}\mathrm{3}{z}+\mathrm{0}.\mathrm{5}{cosz}\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=−\mathrm{0}.\mathrm{5}\left(−\mathrm{1}\right)+\mathrm{0}+\mathrm{0}−\left(−\mathrm{0}.\mathrm{5}+\mathrm{0}.\mathrm{5}+\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{6}−\mathrm{2}}{\mathrm{12}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by Filup last updated on 02/Dec/15
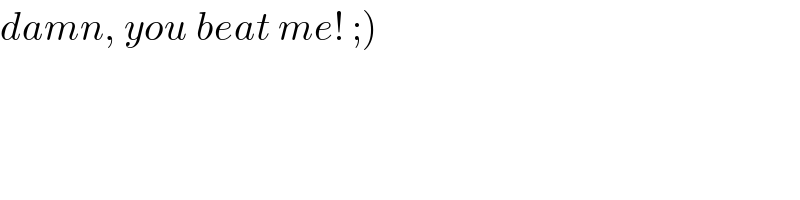
$$\left.{damn},\:{you}\:{beat}\:{me}!\:;\right) \\ $$
Commented by Syaka last updated on 02/Dec/15

$${Thanks}\:{Sir},\:{I}\:{always}\:{learn}\:{from}\:{you}. \\ $$
Answered by Filup last updated on 03/Dec/15
![∫_0 ^(π/2) ∫_0 ^z ∫_0 ^y sin(x+y+z) dx dy dz =∫_0 ^(π/2) ∫_0 ^z −[cos(x+y+z)]_(x=0) ^(x=y) dy dz =∫_0 ^(π/2) ∫_0 ^z (cos(y+z)−cos(2y+z)) dy dz =∫_0 ^(π/2) [sin(y+z)−(1/2)sin(2y+z)]_(y=0) ^(y=z) dz =∫_0 ^(π/2) (sin(2z)−(1/2)sin(3z))−(sin(z)−(1/2)sin(z)) dz =∫_0 ^(π/2) (sin(2z)−(1/2)sin(3z)−(1/2)sin(z)) dz =[−(1/2)cos(2z)+(1/6)cos(3z)+(1/2)cos(z)]_(z=0) ^(z=π/2) =(−(1/2)cos(π)+(1/6)cos(((3π)/2))+(1/2)cos((π/2))) −(−(1/2)cos(0)+(1/6)cos(0)+(1/2)cos(0)) cos(0)=1, cos(nπ)=−1, cos(((nπ)/2))=0, n∈Z =((1/2)+0+0)−(−(1/2)+(1/6)+(1/2)) =(1/2)+(1/2)−(2/3) =1−(2/3) =(1/3) ∴∫_0 ^(π/2) ∫_0 ^z ∫_0 ^y sin(x+y+z) dx dy dz = (1/3)](https://www.tinkutara.com/question/Q2977.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\underset{\mathrm{0}} {\overset{{z}} {\int}}\underset{\mathrm{0}} {\overset{{y}} {\int}}\:\mathrm{sin}\left({x}+{y}+{z}\right)\:{dx}\:{dy}\:{dz} \\ $$$$ \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\underset{\mathrm{0}} {\overset{{z}} {\int}}\:−\left[\mathrm{cos}\left({x}+{y}+{z}\right)\right]_{{x}=\mathrm{0}} ^{{x}={y}} \:{dy}\:{dz} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\underset{\mathrm{0}} {\overset{{z}} {\int}}\:\left(\mathrm{cos}\left({y}+{z}\right)−\mathrm{cos}\left(\mathrm{2}{y}+{z}\right)\right)\:{dy}\:{dz} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\left[\mathrm{sin}\left({y}+{z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}{y}+{z}\right)\right]_{{y}=\mathrm{0}} ^{{y}={z}} \:{dz} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\left(\mathrm{sin}\left(\mathrm{2}{z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{3}{z}\right)\right)−\left(\mathrm{sin}\left({z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left({z}\right)\right)\:{dz} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\left(\mathrm{sin}\left(\mathrm{2}{z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{3}{z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left({z}\right)\right)\:{dz} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2}{z}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\left(\mathrm{3}{z}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left({z}\right)\right]_{{z}=\mathrm{0}} ^{{z}=\pi/\mathrm{2}} \\ $$$$ \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\pi\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$−\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{0}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\left(\mathrm{0}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{0}\right)\right) \\ $$$$ \\ $$$$\mathrm{cos}\left(\mathrm{0}\right)=\mathrm{1},\:\:\:\:\mathrm{cos}\left({n}\pi\right)=−\mathrm{1},\:\:\:\:\mathrm{cos}\left(\frac{{n}\pi}{\mathrm{2}}\right)=\mathrm{0},\:\:\:\:{n}\in\mathbb{Z} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{0}+\mathrm{0}\right)−\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$$\therefore\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\underset{\mathrm{0}} {\overset{{z}} {\int}}\underset{\mathrm{0}} {\overset{{y}} {\int}}\:\mathrm{sin}\left({x}+{y}+{z}\right)\:{dx}\:{dy}\:{dz}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Syaka last updated on 02/Dec/15
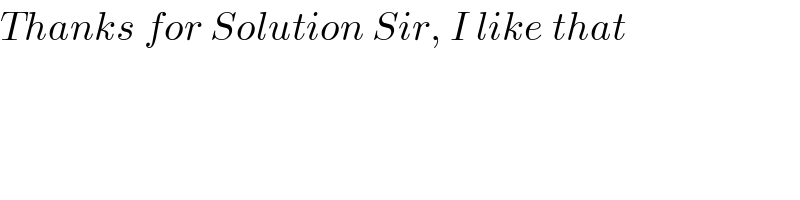
$${Thanks}\:{for}\:{Solution}\:{Sir},\:{I}\:{like}\:{that} \\ $$
