Question Number 31611 by mondodotto@gmail.com last updated on 11/Mar/18
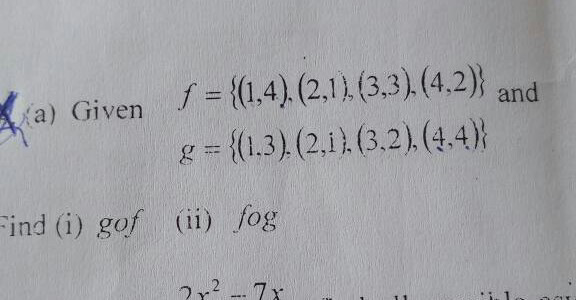
Commented by mondodotto@gmail.com last updated on 11/Mar/18

$$\mathrm{please}\:\mathrm{help} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Mar/18
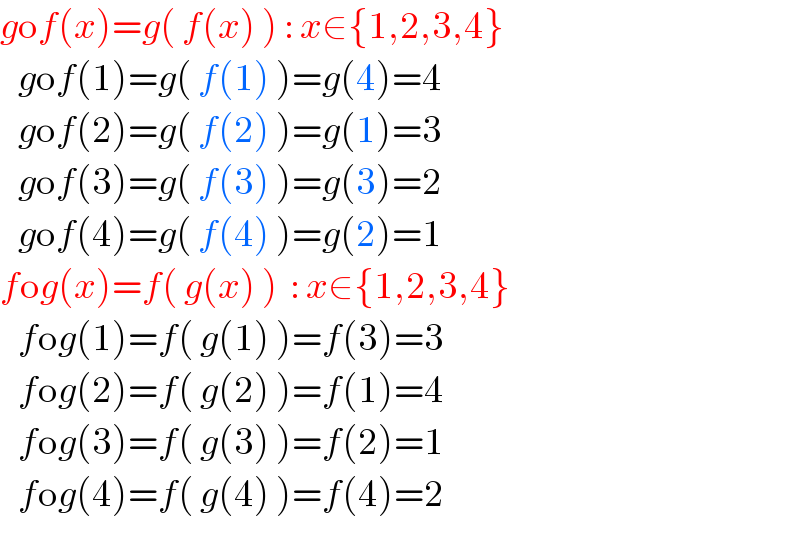
$${g}\mathrm{o}{f}\left({x}\right)={g}\left(\:{f}\left({x}\right)\:\right)\::\:{x}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$$$\:\:\:{g}\mathrm{o}{f}\left(\mathrm{1}\right)={g}\left(\:{f}\left(\mathrm{1}\right)\:\right)={g}\left(\mathrm{4}\right)=\mathrm{4} \\ $$$$\:\:\:{g}\mathrm{o}{f}\left(\mathrm{2}\right)={g}\left(\:{f}\left(\mathrm{2}\right)\:\right)={g}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$\:\:\:{g}\mathrm{o}{f}\left(\mathrm{3}\right)={g}\left(\:{f}\left(\mathrm{3}\right)\:\right)={g}\left(\mathrm{3}\right)=\mathrm{2} \\ $$$$\:\:\:{g}\mathrm{o}{f}\left(\mathrm{4}\right)={g}\left(\:{f}\left(\mathrm{4}\right)\:\right)={g}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$${f}\mathrm{o}{g}\left({x}\right)={f}\left(\:{g}\left({x}\right)\:\right)\:\::\:{x}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$$$\:\:\:{f}\mathrm{o}{g}\left(\mathrm{1}\right)={f}\left(\:{g}\left(\mathrm{1}\right)\:\right)={f}\left(\mathrm{3}\right)=\mathrm{3} \\ $$$$\:\:\:{f}\mathrm{o}{g}\left(\mathrm{2}\right)={f}\left(\:{g}\left(\mathrm{2}\right)\:\right)={f}\left(\mathrm{1}\right)=\mathrm{4} \\ $$$$\:\:\:{f}\mathrm{o}{g}\left(\mathrm{3}\right)={f}\left(\:{g}\left(\mathrm{3}\right)\:\right)={f}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$$\:\:\:{f}\mathrm{o}{g}\left(\mathrm{4}\right)={f}\left(\:{g}\left(\mathrm{4}\right)\:\right)={f}\left(\mathrm{4}\right)=\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Mar/18
![gof [(1,f,4,g,4),(2,f,1,g,3),(3,f,3,g,2),(4,f,2,g,1) ] fog [(1,g,3,f,3),(2,g,1,f,4),(3,g,2,f,1),(4,g,4,f,2) ]](https://www.tinkutara.com/question/Q31621.png)
$${g}\mathrm{o}{f} \\ $$$$\begin{bmatrix}{\mathrm{1}}&{{f}}&{\mathrm{4}}&{{g}}&{\mathrm{4}}\\{\mathrm{2}}&{{f}}&{\mathrm{1}}&{{g}}&{\mathrm{3}}\\{\mathrm{3}}&{{f}}&{\mathrm{3}}&{{g}}&{\mathrm{2}}\\{\mathrm{4}}&{{f}}&{\mathrm{2}}&{{g}}&{\mathrm{1}}\end{bmatrix} \\ $$$${f}\mathrm{o}{g} \\ $$$$\begin{bmatrix}{\mathrm{1}}&{{g}}&{\mathrm{3}}&{{f}}&{\mathrm{3}}\\{\mathrm{2}}&{{g}}&{\mathrm{1}}&{{f}}&{\mathrm{4}}\\{\mathrm{3}}&{{g}}&{\mathrm{2}}&{{f}}&{\mathrm{1}}\\{\mathrm{4}}&{{g}}&{\mathrm{4}}&{{f}}&{\mathrm{2}}\end{bmatrix} \\ $$
Commented by mondodotto@gmail.com last updated on 11/Mar/18
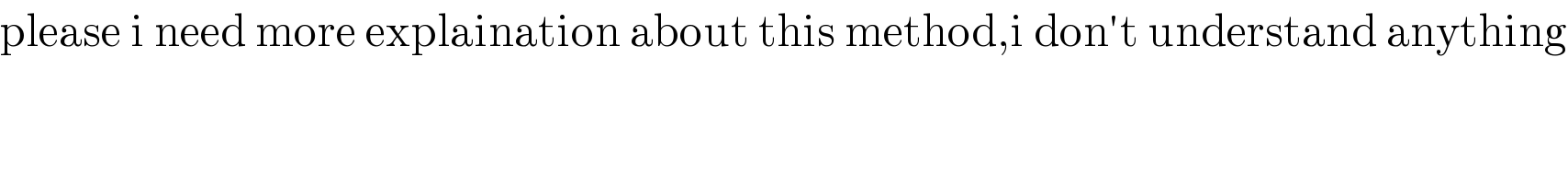
$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{more}\:\mathrm{explaination}\:\mathrm{about}\:\mathrm{this}\:\mathrm{method},\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{anything} \\ $$
Commented by Rasheed.Sindhi last updated on 12/Mar/18
![[(x,f,(f(x)),g,(g( f(x) ))),(1,f,( 4),g,( 4)),(2,f,( 1),g,( 3)),(3,f,( 3),g,( 2)),(4,f,( 2),g,( 1)) ] I have added a guide-row for clarification. Middle column has two roles: it′s output of f and input of g. In the question the function is defined by ordered pairs. First element is input of the function and the second is output which is also called image under the function. (x,y)∈f may also be written x f y x : input of f , y: output of f y is also called image of x under f denoted by f(x).](https://www.tinkutara.com/question/Q31664.png)
$$\begin{bmatrix}{{x}}&{{f}}&{{f}\left({x}\right)}&{{g}}&{{g}\left(\:{f}\left({x}\right)\:\right)}\\{\mathrm{1}}&{{f}}&{\:\:\mathrm{4}}&{{g}}&{\:\:\:\:\:\:\:\mathrm{4}}\\{\mathrm{2}}&{{f}}&{\:\:\mathrm{1}}&{{g}}&{\:\:\:\:\:\:\:\mathrm{3}}\\{\mathrm{3}}&{{f}}&{\:\:\mathrm{3}}&{{g}}&{\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{4}}&{{f}}&{\:\:\mathrm{2}}&{{g}}&{\:\:\:\:\:\:\:\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{added}\:\mathrm{a}\:\mathrm{guide}-\mathrm{row}\:\mathrm{for}\:\mathrm{clarification}. \\ $$$$\mathrm{Middle}\:\mathrm{column}\:\mathrm{has}\:\mathrm{two}\:\mathrm{roles}:\:\mathrm{it}'\mathrm{s}\:\mathrm{output} \\ $$$$\mathrm{of}\:\:{f}\:\:\mathrm{and}\:\mathrm{input}\:\mathrm{of}\:\:{g}. \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{question}\:\mathrm{the}\:\mathrm{function}\:\mathrm{is}\:\mathrm{defined} \\ $$$$\mathrm{by}\:\mathrm{ordered}\:\mathrm{pairs}.\:\mathrm{First}\:\mathrm{element}\:\mathrm{is}\:\mathrm{input} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{and}\:\mathrm{the}\:\mathrm{second}\:\mathrm{is}\:\mathrm{output} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{also}\:\mathrm{called}\:\mathrm{image}\:\mathrm{under}\:\mathrm{the}\:\mathrm{function}. \\ $$$$\:\:\:\:\left(\mathrm{x},\mathrm{y}\right)\in{f}\:\mathrm{may}\:\mathrm{also}\:\mathrm{be}\:\mathrm{written}\:\mathrm{x}\:{f}\:\:\mathrm{y} \\ $$$$\mathrm{x}\::\:\mathrm{input}\:\mathrm{of}\:\:{f}\:,\:\mathrm{y}:\:\mathrm{output}\:\mathrm{of}\:\:{f}\: \\ $$$$\mathrm{y}\:\mathrm{is}\:\mathrm{also}\:\mathrm{called}\:\mathrm{image}\:\mathrm{of}\:\mathrm{x}\:\mathrm{under}\:{f}\:\mathrm{denoted} \\ $$$$\mathrm{by}\:{f}\left(\mathrm{x}\right). \\ $$
Commented by mondodotto@gmail.com last updated on 12/Mar/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
