Question Number 97153 by eidmarie last updated on 06/Jun/20
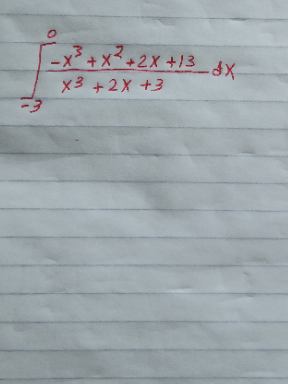
Answered by MJS last updated on 06/Jun/20
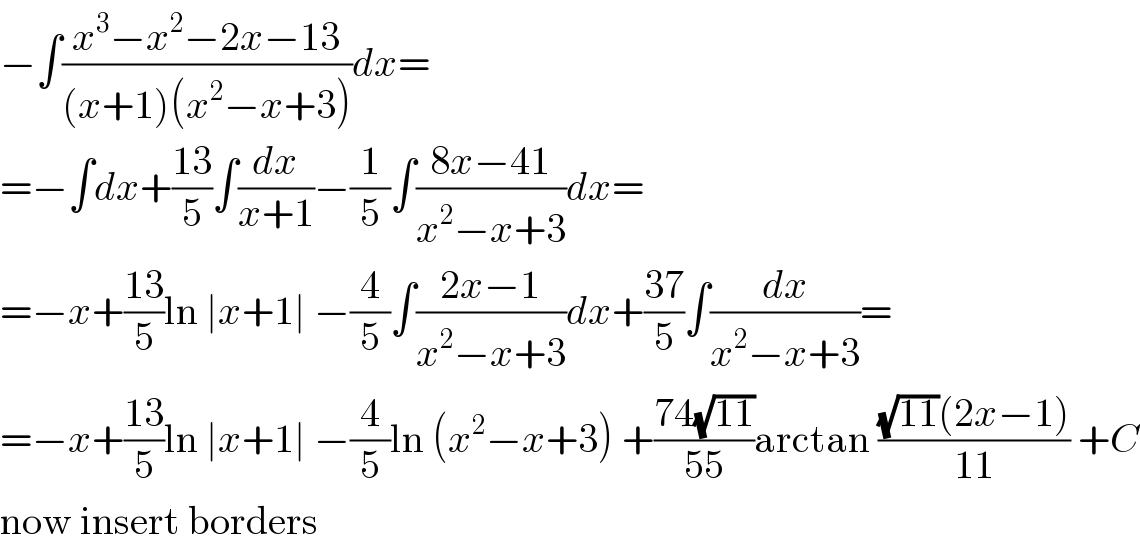
$$−\int\frac{{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{13}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)}{dx}= \\ $$$$=−\int{dx}+\frac{\mathrm{13}}{\mathrm{5}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{8}{x}−\mathrm{41}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{dx}= \\ $$$$=−{x}+\frac{\mathrm{13}}{\mathrm{5}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:−\frac{\mathrm{4}}{\mathrm{5}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}{dx}+\frac{\mathrm{37}}{\mathrm{5}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{3}}= \\ $$$$=−{x}+\frac{\mathrm{13}}{\mathrm{5}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:−\frac{\mathrm{4}}{\mathrm{5}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)\:+\frac{\mathrm{74}\sqrt{\mathrm{11}}}{\mathrm{55}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{11}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{11}}\:+{C} \\ $$$$\mathrm{now}\:\mathrm{insert}\:\mathrm{borders} \\ $$
Answered by mathmax by abdo last updated on 06/Jun/20

$$\mathrm{A}=\int_{−\mathrm{3}} ^{\mathrm{0}} \:\frac{−\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{13}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}+\mathrm{3}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{x}=−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{13}}{−\mathrm{t}^{\mathrm{3}} −\mathrm{2t}\:+\mathrm{3}}\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{13}}{\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}−\mathrm{3}}\mathrm{dt} \\ $$$$\mathrm{A}\:=−\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}−\mathrm{3}\:−\mathrm{2t}+\mathrm{3}+\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{13}}{\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}−\mathrm{3}}\mathrm{dt} \\ $$$$=−\mathrm{3}\:−\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}\:+\mathrm{16}}{\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}−\mathrm{3}}\mathrm{dt}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}\:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{p}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}\:−\mathrm{3} \\ $$$$\mathrm{t}^{\mathrm{3}} \:+\mathrm{2t}−\mathrm{3}\:=\mathrm{t}^{\mathrm{3}} −\mathrm{1}\:+\mathrm{2t}−\mathrm{2}\:=\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right) \\ $$$$=\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}\:+\mathrm{3}\right)\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}\:+\mathrm{16}}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\:+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{1}}\:+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{3}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{13}}{\mathrm{5}}\:\:,\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{1}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=\mathrm{1}−\frac{\mathrm{13}}{\mathrm{5}}\:=−\frac{\mathrm{8}}{\mathrm{5}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=−\frac{\mathrm{16}}{\mathrm{3}}\:=−\mathrm{a}\:+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{a}−\frac{\mathrm{16}}{\mathrm{3}}\:=\frac{\mathrm{13}}{\mathrm{5}}−\frac{\mathrm{16}}{\mathrm{3}}\:=\frac{\mathrm{39}−\mathrm{80}}{\mathrm{15}}\:=−\frac{\mathrm{41}}{\mathrm{15}}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{13}}{\mathrm{5}\left(\mathrm{t}−\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{8}}{\mathrm{5}}\mathrm{t}−\frac{\mathrm{41}}{\mathrm{15}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{3}}\:\:\Rightarrow\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\frac{\mathrm{13}}{\mathrm{5}}\mathrm{ln}\mid\mathrm{t}−\mathrm{1}\mid−\frac{\mathrm{8}}{\mathrm{10}}\:\int\:\:\frac{\mathrm{2t}+\mathrm{1}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{3}}\mathrm{dt} \\ $$$$−\frac{\mathrm{41}}{\mathrm{15}}\:\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{3}}\:\mathrm{now}\:\mathrm{its}\:\mathrm{eazy}\:\mathrm{to}\:\mathrm{solve}…. \\ $$$$ \\ $$
