Question-31639

Question Number 31639 by Tinkutara last updated on 11/Mar/18

Answered by MJS last updated on 11/Mar/18

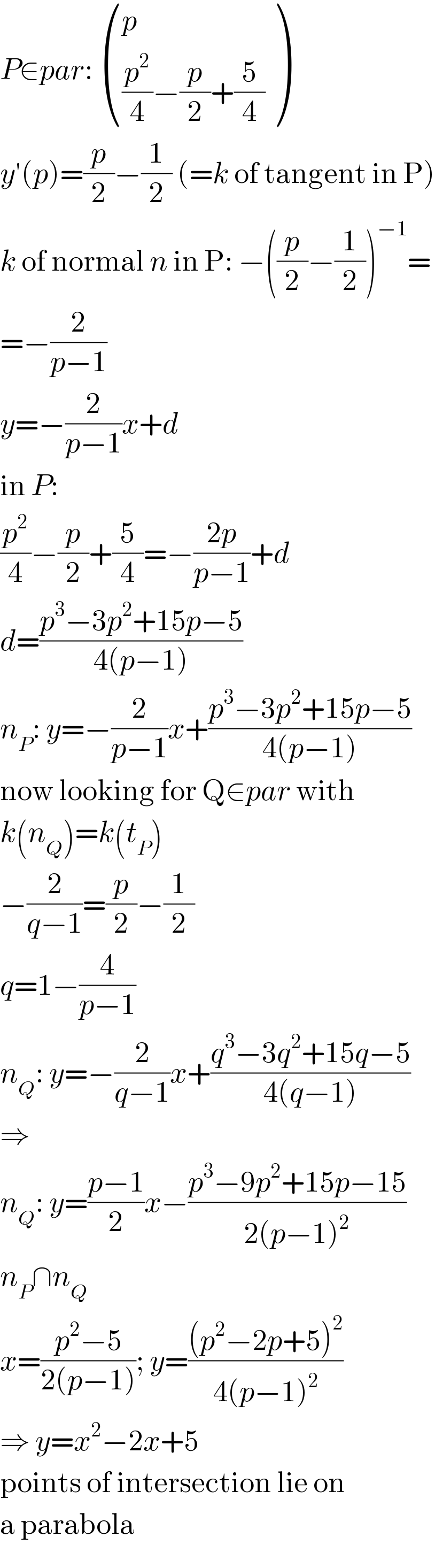
P∈par: ((p),(((p^2 /4)−(p/2)+(5/4))) ) y′(p)=(p/2)−(1/2) (=k of tangent in P) k of normal n in P: −((p/2)−(1/2))^(−1) = =−(2/(p−1)) y=−(2/(p−1))x+d in P: (p^2 /4)−(p/2)+(5/4)=−((2p)/(p−1))+d d=((p^3 −3p^2 +15p−5)/(4(p−1))) n_P : y=−(2/(p−1))x+((p^3 −3p^2 +15p−5)/(4(p−1))) now looking for Q∈par with k(n_Q )=k(t_P ) −(2/(q−1))=(p/2)−(1/2) q=1−(4/(p−1)) n_Q : y=−(2/(q−1))x+((q^3 −3q^2 +15q−5)/(4(q−1))) ⇒ n_Q : y=((p−1)/2)x−((p^3 −9p^2 +15p−15)/(2(p−1)^2 )) n_P ∩n_Q x=((p^2 −5)/(2(p−1))); y=(((p^2 −2p+5)^2 )/(4(p−1)^2 )) ⇒ y=x^2 −2x+5 points of intersection lie on a parabola

$${P}\in{par}:\:\begin{pmatrix}{{p}}\\{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−\frac{{p}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{4}}}\end{pmatrix} \\ $$$${y}'\left({p}\right)=\frac{{p}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:\left(={k}\:\mathrm{of}\:\mathrm{tangent}\:\mathrm{in}\:\mathrm{P}\right) \\ $$$${k}\:\mathrm{of}\:\mathrm{normal}\:{n}\:\mathrm{in}\:\mathrm{P}:\:−\left(\frac{{p}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{1}} = \\ $$$$=−\frac{\mathrm{2}}{{p}−\mathrm{1}} \\ $$$${y}=−\frac{\mathrm{2}}{{p}−\mathrm{1}}{x}+{d} \\ $$$$\mathrm{in}\:{P}: \\ $$$$\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−\frac{{p}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{4}}=−\frac{\mathrm{2}{p}}{{p}−\mathrm{1}}+{d} \\ $$$${d}=\frac{{p}^{\mathrm{3}} −\mathrm{3}{p}^{\mathrm{2}} +\mathrm{15}{p}−\mathrm{5}}{\mathrm{4}\left({p}−\mathrm{1}\right)} \\ $$$${n}_{{P}} :\:{y}=−\frac{\mathrm{2}}{{p}−\mathrm{1}}{x}+\frac{{p}^{\mathrm{3}} −\mathrm{3}{p}^{\mathrm{2}} +\mathrm{15}{p}−\mathrm{5}}{\mathrm{4}\left({p}−\mathrm{1}\right)} \\ $$$$\mathrm{now}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{Q}\in{par}\:\mathrm{with} \\ $$$${k}\left({n}_{{Q}} \right)={k}\left({t}_{{P}} \right) \\ $$$$−\frac{\mathrm{2}}{{q}−\mathrm{1}}=\frac{{p}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${q}=\mathrm{1}−\frac{\mathrm{4}}{{p}−\mathrm{1}} \\ $$$${n}_{{Q}} :\:{y}=−\frac{\mathrm{2}}{{q}−\mathrm{1}}{x}+\frac{{q}^{\mathrm{3}} −\mathrm{3}{q}^{\mathrm{2}} +\mathrm{15}{q}−\mathrm{5}}{\mathrm{4}\left({q}−\mathrm{1}\right)} \\ $$$$\Rightarrow \\ $$$${n}_{{Q}} :\:{y}=\frac{{p}−\mathrm{1}}{\mathrm{2}}{x}−\frac{{p}^{\mathrm{3}} −\mathrm{9}{p}^{\mathrm{2}} +\mathrm{15}{p}−\mathrm{15}}{\mathrm{2}\left({p}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${n}_{{P}} \cap{n}_{{Q}} \\ $$$${x}=\frac{{p}^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}\left({p}−\mathrm{1}\right)};\:{y}=\frac{\left({p}^{\mathrm{2}} −\mathrm{2}{p}+\mathrm{5}\right)^{\mathrm{2}} }{\mathrm{4}\left({p}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:{y}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\mathrm{points}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{lie}\:\mathrm{on} \\ $$$$\mathrm{a}\:\mathrm{parabola} \\ $$

Commented by Tinkutara last updated on 11/Mar/18

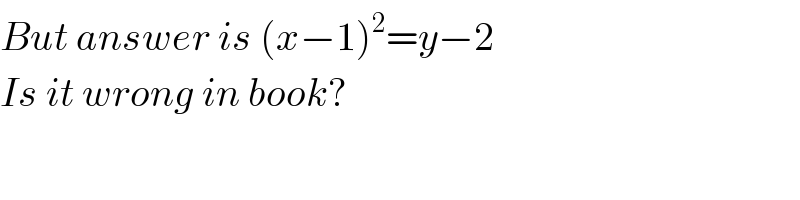
But answer is (x−1)^2 =y−2 Is it wrong in book?

$${But}\:{answer}\:{is}\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} ={y}−\mathrm{2} \\ $$$${Is}\:{it}\:{wrong}\:{in}\:{book}? \\ $$

Commented by MJS last updated on 11/Mar/18

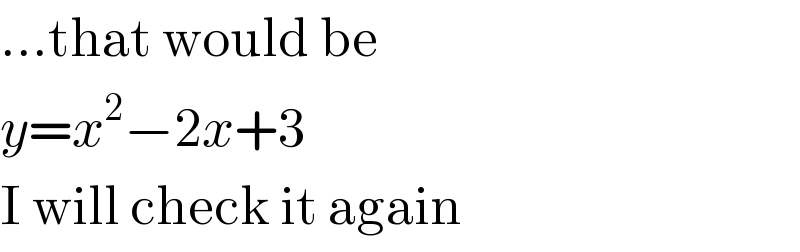
...that would be y=x^2 −2x+3 I will check it again

$$…\mathrm{that}\:\mathrm{would}\:\mathrm{be} \\ $$$${y}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{check}\:\mathrm{it}\:\mathrm{again} \\ $$

Commented by MJS last updated on 11/Mar/18

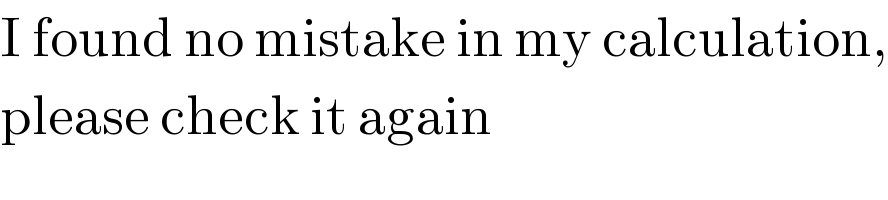
I found no mistake in my calculation, please check it again

$$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{my}\:\mathrm{calculation}, \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{it}\:\mathrm{again} \\ $$

Commented by Tinkutara last updated on 12/Mar/18

I saw again but answer given is only (x−1)^2 =y−2. How to verify which is correct?

$${I}\:{saw}\:{again}\:{but}\:{answer}\:{given}\:{is}\:{only} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} ={y}−\mathrm{2}.\:{How}\:{to}\:{verify}\:{which}\:{is} \\ $$$${correct}? \\ $$

Commented by MJS last updated on 12/Mar/18

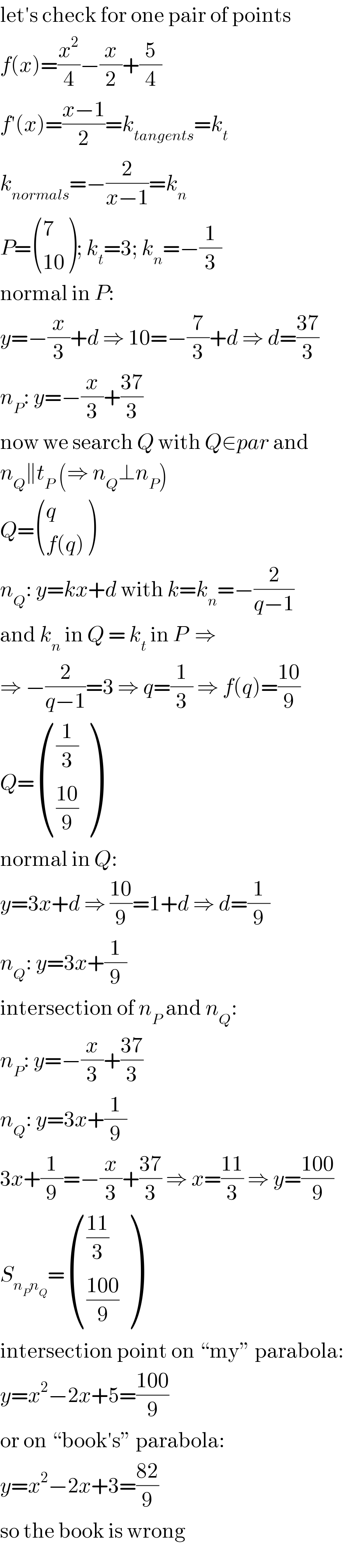
let′s check for one pair of points f(x)=(x^2 /4)−(x/2)+(5/4) f′(x)=((x−1)/2)=k_(tangents) =k_t k_(normals) =−(2/(x−1))=k_n P= ((7),((10)) ); k_t =3; k_n =−(1/3) normal in P: y=−(x/3)+d ⇒ 10=−(7/3)+d ⇒ d=((37)/3) n_P : y=−(x/3)+((37)/3) now we search Q with Q∈par and n_Q ∥t_P (⇒ n_Q ⊥n_P ) Q= ((q),((f(q))) ) n_Q : y=kx+d with k=k_n =−(2/(q−1)) and k_n in Q = k_t in P ⇒ ⇒ −(2/(q−1))=3 ⇒ q=(1/3) ⇒ f(q)=((10)/9) Q= (((1/3)),(((10)/9)) ) normal in Q: y=3x+d ⇒ ((10)/9)=1+d ⇒ d=(1/9) n_Q : y=3x+(1/9) intersection of n_P and n_Q : n_P : y=−(x/3)+((37)/3) n_Q : y=3x+(1/9) 3x+(1/9)=−(x/3)+((37)/3) ⇒ x=((11)/3) ⇒ y=((100)/9) S_(n_P n_Q ) = ((((11)/3)),(((100)/9)) ) intersection point on “my” parabola: y=x^2 −2x+5=((100)/9) or on “book′s” parabola: y=x^2 −2x+3=((82)/9) so the book is wrong

$$\mathrm{let}'\mathrm{s}\:\mathrm{check}\:\mathrm{for}\:\mathrm{one}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{points} \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${f}'\left({x}\right)=\frac{{x}−\mathrm{1}}{\mathrm{2}}={k}_{{tangents}} ={k}_{{t}} \\ $$$${k}_{{normals}} =−\frac{\mathrm{2}}{{x}−\mathrm{1}}={k}_{{n}} \\ $$$${P}=\begin{pmatrix}{\mathrm{7}}\\{\mathrm{10}}\end{pmatrix};\:{k}_{{t}} =\mathrm{3};\:{k}_{{n}} =−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{normal}\:\mathrm{in}\:{P}: \\ $$$${y}=−\frac{{x}}{\mathrm{3}}+{d}\:\Rightarrow\:\mathrm{10}=−\frac{\mathrm{7}}{\mathrm{3}}+{d}\:\Rightarrow\:{d}=\frac{\mathrm{37}}{\mathrm{3}} \\ $$$${n}_{{P}} :\:{y}=−\frac{{x}}{\mathrm{3}}+\frac{\mathrm{37}}{\mathrm{3}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{search}\:{Q}\:\mathrm{with}\:{Q}\in{par}\:\mathrm{and} \\ $$$${n}_{{Q}} \parallel{t}_{{P}} \:\left(\Rightarrow\:{n}_{{Q}} \bot{n}_{{P}} \right) \\ $$$${Q}=\begin{pmatrix}{{q}}\\{{f}\left({q}\right)}\end{pmatrix} \\ $$$${n}_{{Q}} :\:{y}={kx}+{d}\:\mathrm{with}\:{k}={k}_{{n}} =−\frac{\mathrm{2}}{{q}−\mathrm{1}} \\ $$$$\mathrm{and}\:{k}_{{n}} \:\mathrm{in}\:{Q}\:=\:{k}_{{t}} \:\mathrm{in}\:{P}\:\:\Rightarrow \\ $$$$\Rightarrow\:−\frac{\mathrm{2}}{{q}−\mathrm{1}}=\mathrm{3}\:\Rightarrow\:{q}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{f}\left({q}\right)=\frac{\mathrm{10}}{\mathrm{9}} \\ $$$${Q}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{10}}{\mathrm{9}}}\end{pmatrix} \\ $$$$\mathrm{normal}\:\mathrm{in}\:{Q}: \\ $$$${y}=\mathrm{3}{x}+{d}\:\Rightarrow\:\frac{\mathrm{10}}{\mathrm{9}}=\mathrm{1}+{d}\:\Rightarrow\:{d}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${n}_{{Q}} :\:{y}=\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{intersection}\:\mathrm{of}\:{n}_{{P}} \:\mathrm{and}\:{n}_{{Q}} : \\ $$$${n}_{{P}} :\:{y}=−\frac{{x}}{\mathrm{3}}+\frac{\mathrm{37}}{\mathrm{3}} \\ $$$${n}_{{Q}} :\:{y}=\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{9}}=−\frac{{x}}{\mathrm{3}}+\frac{\mathrm{37}}{\mathrm{3}}\:\Rightarrow\:{x}=\frac{\mathrm{11}}{\mathrm{3}}\:\Rightarrow\:{y}=\frac{\mathrm{100}}{\mathrm{9}} \\ $$$${S}_{{n}_{{P}} {n}_{{Q}} } =\begin{pmatrix}{\frac{\mathrm{11}}{\mathrm{3}}}\\{\frac{\mathrm{100}}{\mathrm{9}}}\end{pmatrix} \\ $$$$\mathrm{intersection}\:\mathrm{point}\:\mathrm{on}\:“\mathrm{my}''\:\mathrm{parabola}: \\ $$$${y}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}=\frac{\mathrm{100}}{\mathrm{9}}\: \\ $$$$\mathrm{or}\:\mathrm{on}\:“\mathrm{book}'\mathrm{s}''\:\mathrm{parabola}: \\ $$$${y}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}=\frac{\mathrm{82}}{\mathrm{9}} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{book}\:\mathrm{is}\:\mathrm{wrong} \\ $$

Commented by Tinkutara last updated on 12/Mar/18

Thank you very much Sir! I got the answer. ��

Facebook Tweet Pin

Leave a Reply Cancel reply