Menu Close

Given-n-N-prove-that-k-1-n-k-n-1-k-n-2-3-

Tinku Tara 0 Comments
Pin




Question Number 31713 by gunawan last updated on 13/Mar/18
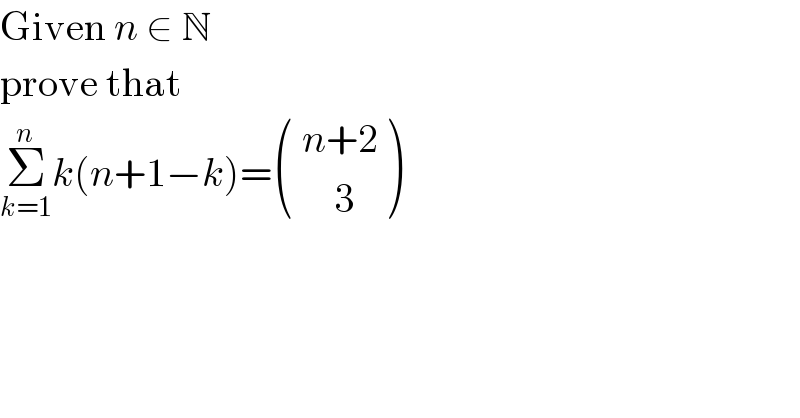
Given n ∈ N prove that Σ_(k=1) ^n k(n+1−k)= ((( n+2)),(( 3)) )
$$\mathrm{Given}\:{n}\:\in\:\mathbb{N} \\ $$$$\mathrm{prove}\:\mathrm{that} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\left({n}+\mathrm{1}−{k}\right)=\begin{pmatrix}{\:{n}+\mathrm{2}}\\{\:\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$
Commented by abdo imad last updated on 13/Mar/18
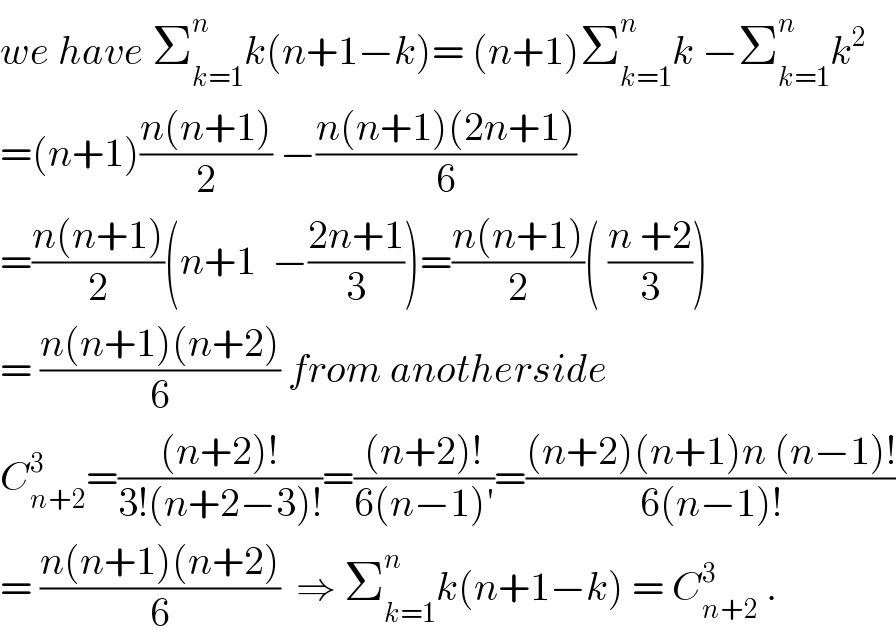
we have Σ_(k=1) ^n k(n+1−k)= (n+1)Σ_(k=1) ^n k −Σ_(k=1) ^n k^2 =(n+1)((n(n+1))/2) −((n(n+1)(2n+1))/6) =((n(n+1))/2)(n+1 −((2n+1)/3))=((n(n+1))/2)( ((n +2)/3)) = ((n(n+1)(n+2))/6) from anotherside C_(n+2) ^3 =(((n+2)!)/(3!(n+2−3)!))=(((n+2)!)/(6(n−1)′))=(((n+2)(n+1)n (n−1)!)/(6(n−1)!)) = ((n(n+1)(n+2))/6) ⇒ Σ_(k=1) ^n k(n+1−k) = C_(n+2) ^3 .
$${we}\:{have}\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left({n}+\mathrm{1}−{k}\right)=\:\left({n}+\mathrm{1}\right)\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:−\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \\ $$$$=\left({n}+\mathrm{1}\right)\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:−\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left({n}+\mathrm{1}\:\:−\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}\right)=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\:\frac{{n}\:+\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=\:\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}}\:{from}\:{anotherside} \\ $$$${C}_{{n}+\mathrm{2}} ^{\mathrm{3}} =\frac{\left({n}+\mathrm{2}\right)!}{\mathrm{3}!\left({n}+\mathrm{2}−\mathrm{3}\right)!}=\frac{\left({n}+\mathrm{2}\right)!}{\mathrm{6}\left({n}−\mathrm{1}\right)'}=\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right){n}\:\left({n}−\mathrm{1}\right)!}{\mathrm{6}\left({n}−\mathrm{1}\right)!} \\ $$$$=\:\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}}\:\:\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left({n}+\mathrm{1}−{k}\right)\:=\:{C}_{{n}+\mathrm{2}} ^{\mathrm{3}} \:. \\ $$
Commented by Tinkutara last updated on 13/Mar/18
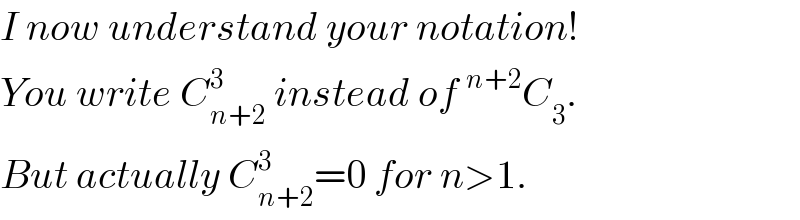
I now understand your notation! You write C_(n+2) ^3 instead of^(n+2) C_3 . But actually C_(n+2) ^3 =0 for n>1.
$${I}\:{now}\:{understand}\:{your}\:{notation}! \\ $$$${You}\:{write}\:{C}_{{n}+\mathrm{2}} ^{\mathrm{3}} \:{instead}\:{of}\:^{{n}+\mathrm{2}} {C}_{\mathrm{3}} . \\ $$$${But}\:{actually}\:{C}_{{n}+\mathrm{2}} ^{\mathrm{3}} =\mathrm{0}\:{for}\:{n}>\mathrm{1}. \\ $$
Commented by abdo imad last updated on 13/Mar/18
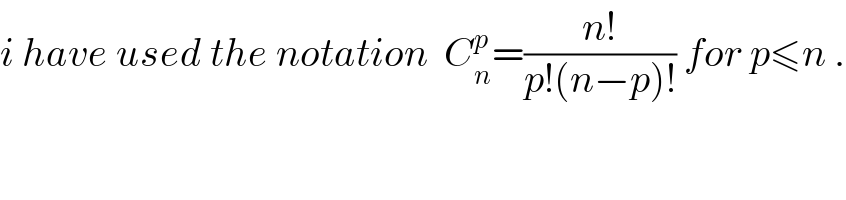
i have used the notation C_n ^p =((n!)/(p!(n−p)!)) for p≤n .
$${i}\:{have}\:{used}\:{the}\:{notation}\:\:{C}_{{n}} ^{{p}} =\frac{{n}!}{{p}!\left({n}−{p}\right)!}\:{for}\:{p}\leqslant{n}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *