Question Number 97270 by bobhans last updated on 07/Jun/20
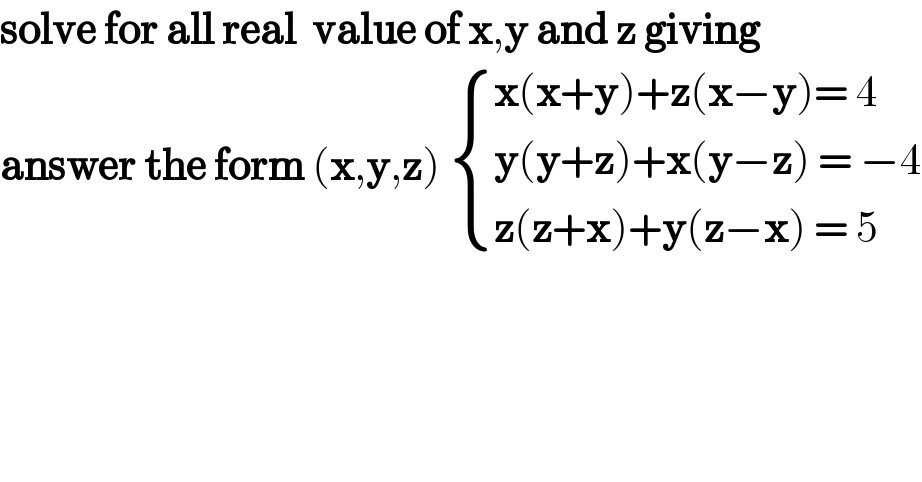
$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{real}}\:\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{z}}\:\boldsymbol{\mathrm{giving}} \\ $$$$\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{form}}\:\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}},\boldsymbol{\mathrm{z}}\right)\:\begin{cases}{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)+\boldsymbol{\mathrm{z}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)=\:\mathrm{4}}\\{\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{z}}\right)+\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{z}}\right)\:=\:−\mathrm{4}}\\{\boldsymbol{\mathrm{z}}\left(\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{z}}−\boldsymbol{\mathrm{x}}\right)\:=\:\mathrm{5}}\end{cases} \\ $$
Commented by john santu last updated on 07/Jun/20

$$\left(\mathrm{1}\right)\:\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{xz}−\mathrm{yz}\:=\:\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{y}^{\mathrm{2}} +\mathrm{xy}−\mathrm{xz}+\mathrm{yz}\:=\:−\mathrm{4} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{z}^{\mathrm{2}} −\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\:=\:\mathrm{5} \\ $$$$\mathrm{adding}\:\left(\mathrm{1}\right),\left(\mathrm{2}\right)\:\Rightarrow\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{0}\:,\mathrm{x}+\mathrm{y}\:=\:\mathrm{0}\:\left(\mathrm{4}\right) \\ $$$$\mathrm{adding}\:\left(\mathrm{2}\right),\left(\mathrm{3}\right)\Rightarrow\:\left(\mathrm{z}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{1}\:,\mathrm{z}+\mathrm{y}=\:\pm\:\mathrm{1}\left(\mathrm{5}\right) \\ $$$$\mathrm{adding}\:\left(\mathrm{1}\right),\left(\mathrm{3}\right)\Rightarrow\:\left(\mathrm{x}+\mathrm{z}\right)^{\mathrm{2}} =\:\mathrm{9},\:\mathrm{x}+\mathrm{z}\:=\:\pm\:\mathrm{3}\:\left(\mathrm{6}\right) \\ $$$$\mathrm{from}\:\left(\mathrm{4}\right)+\left(\mathrm{5}\right)+\left(\mathrm{6}\right)\: \\ $$$$\mathrm{2x}+\mathrm{2y}+\mathrm{2z}\:=\:\mathrm{4}\:\mathrm{or} \\ $$$$\mathrm{2x}+\mathrm{2y}+\mathrm{2z}\:=\:\mathrm{2}\:\mathrm{or} \\ $$$$\mathrm{2x}+\mathrm{2y}+\mathrm{2z}\:=\:−\mathrm{4}\: \\ $$$$\mathrm{2x}+\mathrm{2y}+\mathrm{2z}\:=\:−\mathrm{2} \\ $$$$\begin{cases}{\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{2},\:\mathrm{z}\:=\:\mathrm{2}\:\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{1},\:\mathrm{3}}\\{\mathrm{y}=−\mathrm{1},−\mathrm{3}}\end{cases}}\\{\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1},\:\mathrm{z}=\mathrm{1}\:\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{0},\mathrm{2}}\\{\mathrm{y}=\mathrm{0},−\mathrm{2}}\end{cases}}\\{\mathrm{x}+\mathrm{y}+\mathrm{z}=−\mathrm{2},\mathrm{z}=−\mathrm{2}\Rightarrow\begin{cases}{\mathrm{x}=−\mathrm{3},−\mathrm{1}}\\{\mathrm{y}=\mathrm{3},\mathrm{1}}\end{cases}}\\{\mathrm{x}+\mathrm{y}+\mathrm{z}=−\mathrm{1},\mathrm{z}=−\mathrm{1}\Rightarrow\begin{cases}{\mathrm{x}=−\mathrm{2},\mathrm{0}}\\{\mathrm{y}=\mathrm{2},\mathrm{0}}\end{cases}}\end{cases} \\ $$
Commented by john santu last updated on 07/Jun/20
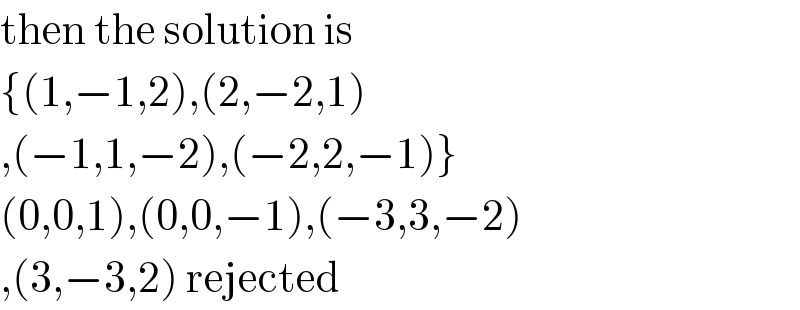
$$\mathrm{then}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\: \\ $$$$\left\{\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},−\mathrm{2},\mathrm{1}\right)\right. \\ $$$$\left.,\left(−\mathrm{1},\mathrm{1},−\mathrm{2}\right),\left(−\mathrm{2},\mathrm{2},−\mathrm{1}\right)\right\} \\ $$$$\left(\mathrm{0},\mathrm{0},\mathrm{1}\right),\left(\mathrm{0},\mathrm{0},−\mathrm{1}\right),\left(−\mathrm{3},\mathrm{3},−\mathrm{2}\right)\: \\ $$$$,\left(\mathrm{3},−\mathrm{3},\mathrm{2}\right)\:\mathrm{rejected} \\ $$
Commented by bobhans last updated on 07/Jun/20

$$\mathrm{thank}\:\mathrm{you}=\:\mathrm{correct}\:\mathrm{sir} \\ $$
Answered by 1549442205 last updated on 07/Jun/20
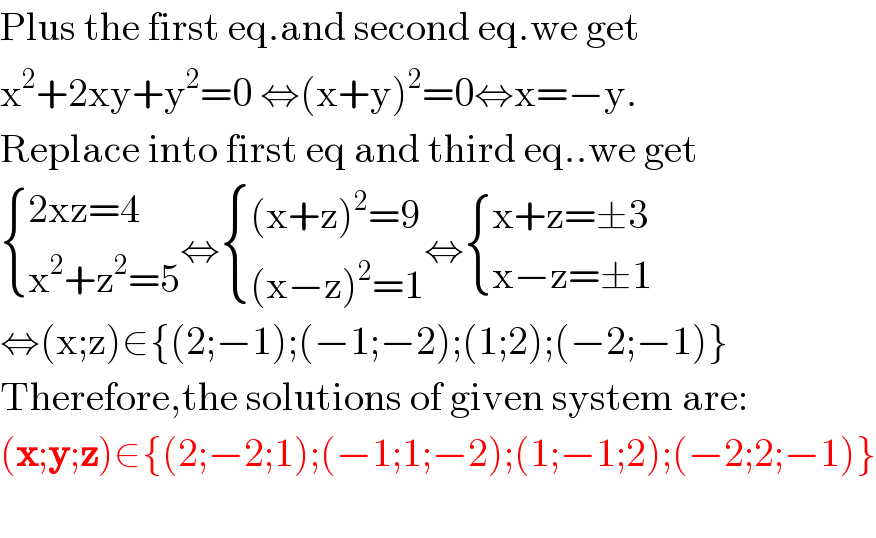
$$\mathrm{Plus}\:\mathrm{the}\:\mathrm{first}\:\mathrm{eq}.\mathrm{and}\:\mathrm{second}\:\mathrm{eq}.\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{0}\:\Leftrightarrow\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{0}\Leftrightarrow\mathrm{x}=−\mathrm{y}. \\ $$$$\mathrm{Replace}\:\mathrm{into}\:\mathrm{first}\:\mathrm{eq}\:\mathrm{and}\:\mathrm{third}\:\mathrm{eq}..\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\mathrm{2xz}=\mathrm{4}}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{5}}\end{cases}\Leftrightarrow\begin{cases}{\left(\mathrm{x}+\mathrm{z}\right)^{\mathrm{2}} =\mathrm{9}}\\{\left(\mathrm{x}−\mathrm{z}\right)^{\mathrm{2}} =\mathrm{1}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{z}=\pm\mathrm{3}}\\{\mathrm{x}−\mathrm{z}=\pm\mathrm{1}}\end{cases} \\ $$$$\Leftrightarrow\left(\mathrm{x};\mathrm{z}\right)\in\left\{\left(\mathrm{2};−\mathrm{1}\right);\left(−\mathrm{1};−\mathrm{2}\right);\left(\mathrm{1};\mathrm{2}\right);\left(−\mathrm{2};−\mathrm{1}\right)\right\} \\ $$$$\mathrm{Therefore},\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{given}\:\mathrm{system}\:\mathrm{are}: \\ $$$$\left(\boldsymbol{\mathrm{x}};\boldsymbol{\mathrm{y}};\boldsymbol{\mathrm{z}}\right)\in\left\{\left(\mathrm{2};−\mathrm{2};\mathrm{1}\right);\left(−\mathrm{1};\mathrm{1};−\mathrm{2}\right);\left(\mathrm{1};−\mathrm{1};\mathrm{2}\right);\left(−\mathrm{2};\mathrm{2};−\mathrm{1}\right)\right\} \\ $$$$ \\ $$
Commented by bemath last updated on 07/Jun/20

$$\mathrm{yess} \\ $$
Commented by bobhans last updated on 07/Jun/20

$$\mathrm{yess} \\ $$
