Question Number 2983 by Syaka last updated on 02/Dec/15
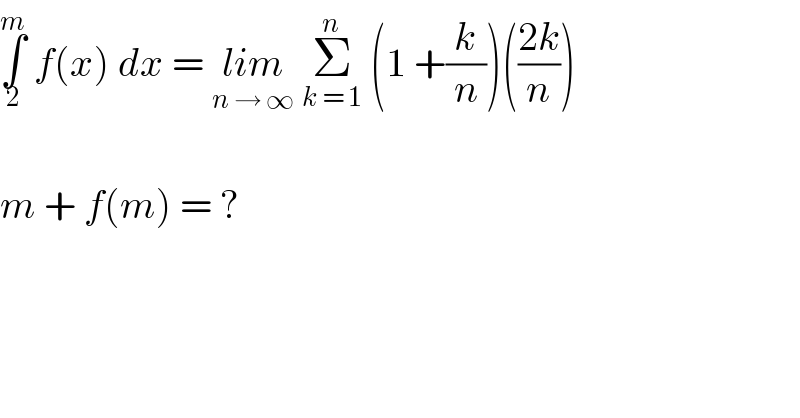
$$\underset{\mathrm{2}} {\overset{{m}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\underset{{n}\:\rightarrow\:\infty} {{lim}}\:\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\mathrm{1}\:+\frac{{k}}{{n}}\right)\left(\frac{\mathrm{2}{k}}{{n}}\right) \\ $$$$ \\ $$$${m}\:+\:{f}\left({m}\right)\:=\:? \\ $$
Commented by prakash jain last updated on 03/Dec/15
![Σ_(k=1) ^n (((2k)/n)+((2k^2 )/n^2 ))=(2/n)Σ_(k=1) ^n k+(2/n^2 )Σ_(k=1) ^n k^2 = (2/n)∙((n(n+1))/2)+(2/n^2 )∙((n(n+1)(2n+1))/6) ∫_0 ^m f(x)dx=lim_(n→∞) [(n+1)+((2n)/3)+1+(1/n)]](https://www.tinkutara.com/question/Q2997.png)
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{2}{k}}{{n}}+\frac{\mathrm{2}{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)=\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}+\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} = \\ $$$$\:\:\:\:\frac{\mathrm{2}}{{n}}\centerdot\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\centerdot\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$\int_{\mathrm{0}} ^{{m}} {f}\left({x}\right){dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\left({n}+\mathrm{1}\right)+\frac{\mathrm{2}{n}}{\mathrm{3}}+\mathrm{1}+\frac{\mathrm{1}}{{n}}\right] \\ $$
