Question Number 97423 by mathmax by abdo last updated on 08/Jun/20
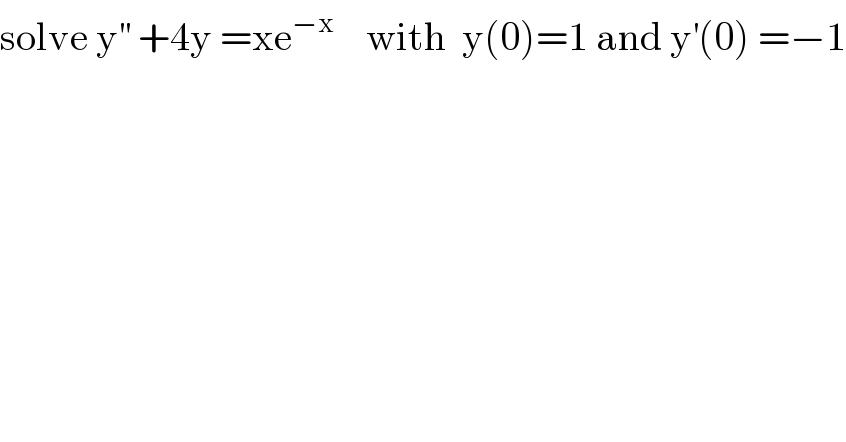
$$\mathrm{solve}\:\mathrm{y}^{''} \:+\mathrm{4y}\:=\mathrm{xe}^{−\mathrm{x}} \:\:\:\:\mathrm{with}\:\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)\:=−\mathrm{1} \\ $$
Answered by Rio Michael last updated on 08/Jun/20

$${m}^{\mathrm{2}} \:+\:\mathrm{4}\:=\:\mathrm{0}\:\Leftrightarrow\:{m}\:=\:\pm\mathrm{2}{i}\:\Rightarrow\:{y}_{{c}} \:=\:\left({A}\mathrm{cos}\:\mathrm{2}{x}\:+{B}\:\mathrm{sin}\:\mathrm{2}{x}\right) \\ $$$$\mathrm{let}\:{y}\:=\:{Cxe}^{−{x}} \:+\:{De}^{−{x}} \:\Rightarrow\:{y}'\:=\:−{Cxe}^{−{x}} \:+\:{Ce}^{−{x}} −{De}^{−{x}} \\ $$$$\Rightarrow\:{y}''\:=\:{Cxe}^{−{x}} \:−{Ce}^{−{x}} −{Ce}^{−{x}} +\:{De}^{−{x}} \:=\:{Cxe}^{−{x}} −\mathrm{2}{Ce}^{−{x}} \:+\:{De}^{−{x}} \\ $$$$\Rightarrow\:{Cxe}^{−{x}} −\mathrm{2}{Ce}^{−{x}} \:+\:{De}^{−{x}} \:=\:{xe}^{−{x}} \\ $$$$\:{Cx}−\mathrm{2}{C}\:+\:{D}\:=\:{x} \\ $$$$\Rightarrow\:\:\left({C}−\mathrm{1}\right){x}−\mathrm{2}{C}\:+\:{D}\:=\:\mathrm{0}\:\Rightarrow\:{C}\:=\:\mathrm{1}\:\mathrm{and}\:−\mathrm{2}{C}\:+{D}\:=\:\mathrm{0}\:\Rightarrow\:{D}\:=\:\mathrm{2} \\ $$$${y}_{{g}} \:=\:{A}\:\mathrm{cos}\:\mathrm{2}{x}\:+\:{B}\mathrm{sin}\:\mathrm{2}{x}\:+\:{xe}^{−{x}} \:+\:\mathrm{2}{e}^{−{x}} \\ $$$${y}\:=\:\mathrm{1},\:{x}\:=\:\mathrm{0}\:\Rightarrow\:\:\mathrm{1}\:=\:{A}\:+\:\mathrm{2}\:\Rightarrow\:\boldsymbol{{A}}\:=\:−\mathrm{1} \\ $$$${y}'\:=\:−\mathrm{2}{A}\mathrm{sin}\:\mathrm{2}{x}\:+\:\mathrm{2}{B}\mathrm{cos}\:\mathrm{2}{x}\:−{xe}^{−{x}} \:+\:{e}^{−{x}} \:−\mathrm{2}{e}^{−{x}} \\ $$$${y}'\:=\:−\mathrm{1}\:,\:{x}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{2}{B}\:\:+\:\mathrm{1}\:−\mathrm{2}\:=\:−\mathrm{1}\:\Rightarrow\:\boldsymbol{{B}}\:=\:\mathrm{0} \\ $$$${y}\:=\:−\mathrm{cos}\:\mathrm{2}{x}\:+\:{xe}^{−{x}} \:+\:\mathrm{2}{e}^{−{x}} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$
Answered by mathmax by abdo last updated on 08/Jun/20
![let solve by laplace transform (e)⇒L(y^(′′) )+4L(y) =L(xe^(−x) ) ⇒x^2 L(y)−xy(0)−y^′ (0)+4L(y) =L(xe^(−x) ) ⇒(x^2 +4)L(y)−x+1 =L(xe^(−x) ) ⇒(x^2 +4)L(y) =x−1 +L(xe^(−x) ) we have L(xe^(−x) ) =∫_0 ^∞ t e^(−t) e^(−xt) dt =∫_0 ^∞ t e^(−(x+1)t) dt =_(by parts) [−(1/(x+1)) e^(−(x+1)t) ]_0 ^∞ +∫_0 ^∞ (1/(x+1)) e^(−(x+1)t) dt =(1/(x+1)) +(1/(x+1))[−(1/(x+1)) e^(−(x+1)t) ]_0 ^∞ =(1/(x+1)) +(1/((x+1)^2 )) ⇒ (x^2 +4)L(y) =x−1 +(1/(x+1)) +(1/((x+1)^2 )) ⇒L(y) =((x−1)/(x^2 +4)) +(1/((x+1)(x^2 +4))) +(1/((x+1)^2 (x^2 +4))) ⇒y(x) =L^(−1) (((x−1)/(x^2 +4)))+L^(−1) ((1/((x+1)(x^2 +4))))+L^(−1) ((1/((x+1)^2 (x^2 +4)))) f(x) =((x−1)/(x^2 +4)) =((x−1)/((x−2i)(x+2i))) =(a/(x−2i)) +(b/(x+2i)) a =((2i−1)/(4i)) =(1/2) +(i/4) and b =((−2i−1)/(−4i)) =((2i+1)/(4i)) =(1/2) +(1/(4i))=(1/2)−(i/4) ⇒ f(x) =((1/2) +(i/4))×(1/(x−2i)) +((1/2)−(i/4))×(1/(x+2i)) L^(−1) (f(x)) =((1/2)+(i/4))e^(2ix) +((1/2)−(i/4))e^(−2ix) (→at form acos(2x)+bsin(2x)) g(x) =(1/((x+1)(x^2 +4))) =(1/((x+1)(x−2i)(x+2i))) =(a/(x+1)) +(b/(x−2i)) +(c/(x+2i)) a =(1/((−1−2i)i)) =(i/((1+2i))) b =(1/((2i+1)4i)) =((−i)/(4(2i+1))) and c =(1/((−2i+1)(−4i))) =(1/(4i(2i−1))) =((−i)/(4(2i−1))) L^(−1) (g(x)) =ae^(−x) +b e^(2ix) +c e^(−2ix) (→ae^(−x) +αcos(2x)+βsin(2x)) h(x) =(1/((x+1)^2 (x^2 +4))) =(a/(x+1)) +(b/((x+1)^2 )) +(c/(x+2i)) +(d/(x−2i)) ⇒ L^(−1) (h) =ae^(−x) +bx e^(−x) +c e^(−2ix) +d e^(2ix) (→at form( a +bx)e^(−x) +αcos(2x) +bsin(2x) .....](https://www.tinkutara.com/question/Q97536.png)
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform}\: \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{4L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{xe}^{−\mathrm{x}} \right)\:\Rightarrow\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)+\mathrm{4L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{xe}^{−\mathrm{x}} \right) \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}+\mathrm{1}\:=\mathrm{L}\left(\mathrm{xe}^{−\mathrm{x}} \right)\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{x}−\mathrm{1}\:+\mathrm{L}\left(\mathrm{xe}^{−\mathrm{x}} \right)\: \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{L}\left(\mathrm{xe}^{−\mathrm{x}} \right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\mathrm{t}} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\left[−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\left[−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{x}−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\:=\frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}−\mathrm{2i}\right)\left(\mathrm{x}+\mathrm{2i}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{2i}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{2i}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{2i}−\mathrm{1}}{\mathrm{4i}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{i}}{\mathrm{4}}\:\:\mathrm{and}\:\mathrm{b}\:=\frac{−\mathrm{2i}−\mathrm{1}}{−\mathrm{4i}}\:=\frac{\mathrm{2i}+\mathrm{1}}{\mathrm{4i}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4i}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{i}}{\mathrm{4}}\right)×\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2i}}\:+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{4}}\right)×\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2i}} \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}}{\mathrm{4}}\right)\mathrm{e}^{\mathrm{2ix}} \:+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{4}}\right)\mathrm{e}^{−\mathrm{2ix}} \:\left(\rightarrow\mathrm{at}\:\mathrm{form}\:\mathrm{acos}\left(\mathrm{2x}\right)+\mathrm{bsin}\left(\mathrm{2x}\right)\right) \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2i}\right)\left(\mathrm{x}+\mathrm{2i}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{x}−\mathrm{2i}}\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{2i}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\left(−\mathrm{1}−\mathrm{2i}\right)\mathrm{i}}\:=\frac{\mathrm{i}}{\left(\mathrm{1}+\mathrm{2i}\right)} \\ $$$$\mathrm{b}\:=\frac{\mathrm{1}}{\left(\mathrm{2i}+\mathrm{1}\right)\mathrm{4i}}\:=\frac{−\mathrm{i}}{\mathrm{4}\left(\mathrm{2i}+\mathrm{1}\right)}\:\:\mathrm{and}\:\mathrm{c}\:=\frac{\mathrm{1}}{\left(−\mathrm{2i}+\mathrm{1}\right)\left(−\mathrm{4i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4i}\left(\mathrm{2i}−\mathrm{1}\right)}\:=\frac{−\mathrm{i}}{\mathrm{4}\left(\mathrm{2i}−\mathrm{1}\right)} \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{g}\left(\mathrm{x}\right)\right)\:=\mathrm{ae}^{−\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{2ix}} \:+\mathrm{c}\:\mathrm{e}^{−\mathrm{2ix}} \:\left(\rightarrow\mathrm{ae}^{−\mathrm{x}} \:+\alpha\mathrm{cos}\left(\mathrm{2x}\right)+\beta\mathrm{sin}\left(\mathrm{2x}\right)\right) \\ $$$$\mathrm{h}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{b}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{2i}}\:+\frac{\mathrm{d}}{\mathrm{x}−\mathrm{2i}}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{h}\right)\:=\mathrm{ae}^{−\mathrm{x}} \:+\mathrm{bx}\:\mathrm{e}^{−\mathrm{x}} \:+\mathrm{c}\:\mathrm{e}^{−\mathrm{2ix}} \:+\mathrm{d}\:\mathrm{e}^{\mathrm{2ix}} \:\left(\rightarrow\mathrm{at}\:\mathrm{form}\left(\:\mathrm{a}\:+\mathrm{bx}\right)\mathrm{e}^{−\mathrm{x}} +\alpha\mathrm{cos}\left(\mathrm{2x}\right)\:+\mathrm{bsin}\left(\mathrm{2x}\right)\right. \\ $$$$….. \\ $$$$ \\ $$
