Question Number 163028 by BHOOPENDRA last updated on 03/Jan/22
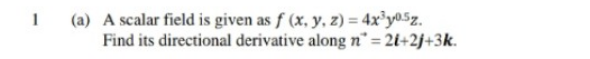
Answered by aleks041103 last updated on 03/Jan/22
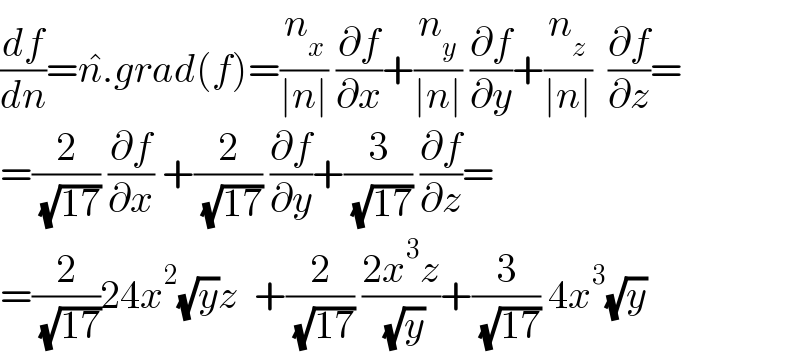
$$\frac{{df}}{{dn}}=\hat {{n}}.{grad}\left({f}\right)=\frac{{n}_{{x}} }{\mid{n}\mid}\:\frac{\partial{f}}{\partial{x}}+\frac{{n}_{{y}} }{\mid{n}\mid}\:\frac{\partial{f}}{\partial{y}}+\frac{{n}_{{z}} }{\mid{n}\mid}\:\:\frac{\partial{f}}{\partial{z}}= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{17}}}\:\frac{\partial{f}}{\partial{x}}\:+\frac{\mathrm{2}}{\:\sqrt{\mathrm{17}}}\:\frac{\partial{f}}{\partial{y}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{17}}}\:\frac{\partial{f}}{\partial{z}}= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{17}}}\mathrm{24}{x}^{\mathrm{2}} \sqrt{{y}}{z}\:\:+\frac{\mathrm{2}}{\:\sqrt{\mathrm{17}}}\:\frac{\mathrm{2}{x}^{\mathrm{3}} {z}}{\:\sqrt{{y}}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{17}}}\:\mathrm{4}{x}^{\mathrm{3}} \sqrt{{y}} \\ $$
