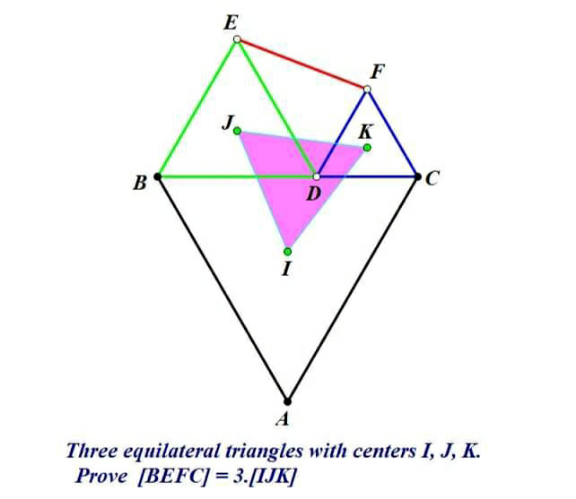
Question Number 163100 by HongKing last updated on 03/Jan/22
Answered by mr W last updated on 04/Jan/22
Commented by mr W last updated on 04/Jan/22
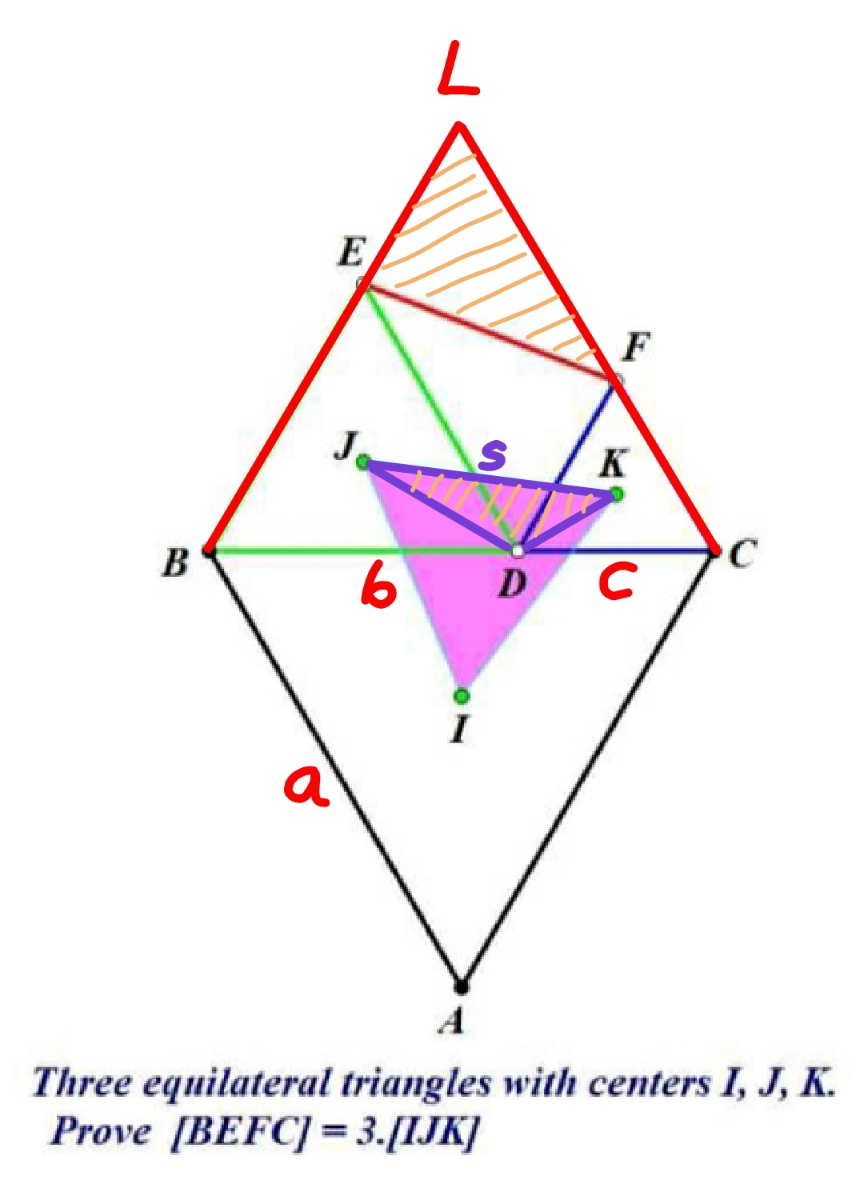
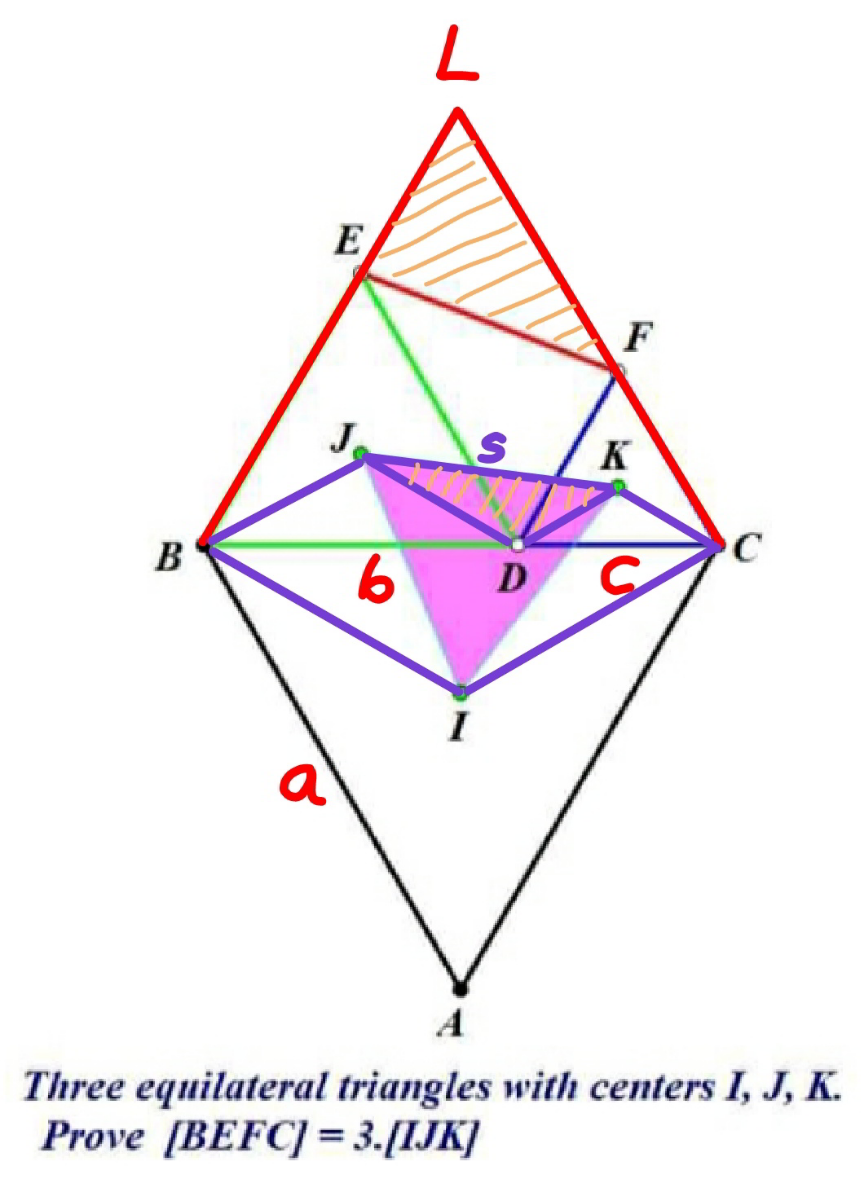
![say the three equilateral triangles have side lengthes a,b,c. a=b+c ΔBCL=ΔBCA [BCL]=[ABC]=(((√3)a^2 )/4) LE=a−b LF=a−c [LEF]=(((a−b)(a−c)sin 60°)/2)=(((√3)(a−b)(a−c))/4) [BEFC]=[BCL]−[LEF] =((√3)/4)[a^2 −(a−b)(a−c)] =((√3)/4)[(b+c)^2 −cb] =((√3)/4)(b^2 +c^2 +bc) DJ=(2/3)×(((√3)b)/2)=(((√3)b)/3) DK=(2/3)×(((√3)c)/2)=(((√3)c)/3) ∠JDK=120° side length of ΔIJK=s s^2 =((((√3)b)/3))^2 +((((√3)c)/3))^2 +2((((√3)b)/3))((((√3)c)/3))(1/2) s^2 =((b^2 +c^2 +bc)/3) [IJK]=(((√3)s^2 )/4)=(1/3)×(((√3)(b^2 +c^2 +bc))/4)=(([BEFC])/3) ⇒[BEFC]=3[IJK] ✓ note: ΔIJK is also equilateral. this can be easily proved, maybe somewhere else later.](https://www.tinkutara.com/question/Q163124.png)
$${say}\:{the}\:{three}\:{equilateral}\:{triangles} \\ $$$${have}\:{side}\:{lengthes}\:{a},{b},{c}.\: \\ $$$${a}={b}+{c} \\ $$$$\Delta{BCL}=\Delta{BCA} \\ $$$$\left[{BCL}\right]=\left[{ABC}\right]=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${LE}={a}−{b} \\ $$$${LF}={a}−{c} \\ $$$$\left[{LEF}\right]=\frac{\left({a}−{b}\right)\left({a}−{c}\right)\mathrm{sin}\:\mathrm{60}°}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}\left({a}−{b}\right)\left({a}−{c}\right)}{\mathrm{4}} \\ $$$$\left[{BEFC}\right]=\left[{BCL}\right]−\left[{LEF}\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[{a}^{\mathrm{2}} −\left({a}−{b}\right)\left({a}−{c}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left({b}+{c}\right)^{\mathrm{2}} −{cb}\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right) \\ $$$${DJ}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}} \\ $$$${DK}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{3}} \\ $$$$\angle{JDK}=\mathrm{120}° \\ $$$${side}\:{length}\:{of}\:\Delta{IJK}={s} \\ $$$${s}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)\left(\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{3}}\right)\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}}{\mathrm{3}} \\ $$$$\left[{IJK}\right]=\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right)}{\mathrm{4}}=\frac{\left[{BEFC}\right]}{\mathrm{3}} \\ $$$$\Rightarrow\left[{BEFC}\right]=\mathrm{3}\left[{IJK}\right]\:\checkmark \\ $$$$ \\ $$$${note}:\:\Delta{IJK}\:{is}\:{also}\:{equilateral}.\:{this} \\ $$$${can}\:{be}\:{easily}\:{proved},\:{maybe}\: \\ $$$${somewhere}\:{else}\:{later}. \\ $$
Commented by mr W last updated on 04/Jan/22
Commented by Tawa11 last updated on 04/Jan/22

$$\mathrm{Wow}\:\mathrm{great}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 04/Jan/22
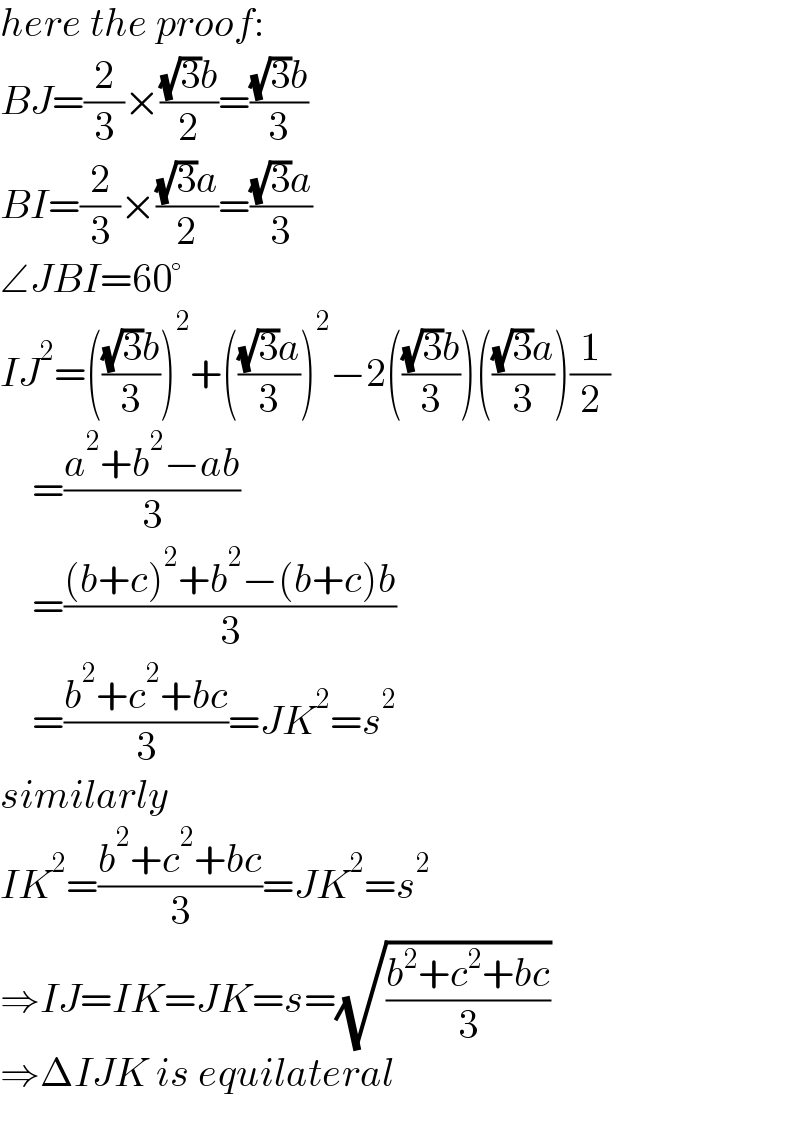
$${here}\:{the}\:{proof}: \\ $$$${BJ}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}} \\ $$$${BI}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$$\angle{JBI}=\mathrm{60}° \\ $$$${IJ}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}}\right)\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}}\right)\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}}{\mathrm{3}} \\ $$$$\:\:\:\:=\frac{\left({b}+{c}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({b}+{c}\right){b}}{\mathrm{3}} \\ $$$$\:\:\:\:=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}}{\mathrm{3}}={JK}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$${similarly} \\ $$$${IK}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}}{\mathrm{3}}={JK}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\Rightarrow{IJ}={IK}={JK}={s}=\sqrt{\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}}{\mathrm{3}}} \\ $$$$\Rightarrow\Delta{IJK}\:{is}\:{equilateral} \\ $$
Commented by HongKing last updated on 04/Jan/22
$$\mathrm{perfect}\:\mathrm{solution}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
