Question Number 134102 by mnjuly1970 last updated on 27/Feb/21
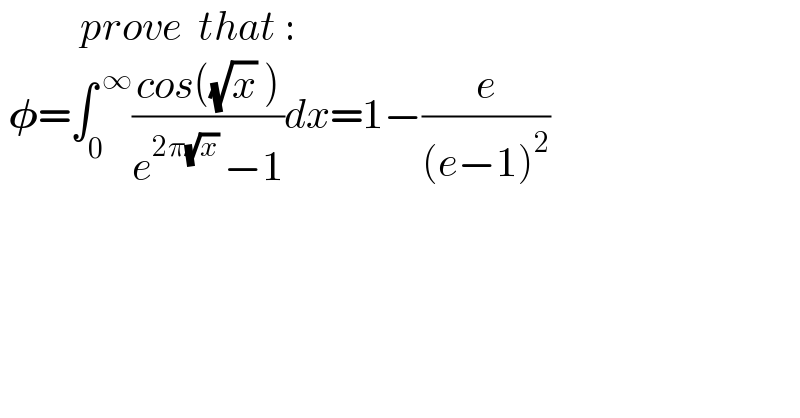
$$\:\:\:\:\:\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left(\sqrt{{x}}\:\right)}{{e}^{\mathrm{2}\pi\sqrt{{x}}\:} −\mathrm{1}}{dx}=\mathrm{1}−\frac{{e}}{\left({e}−\mathrm{1}\right)_{} ^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 27/Feb/21
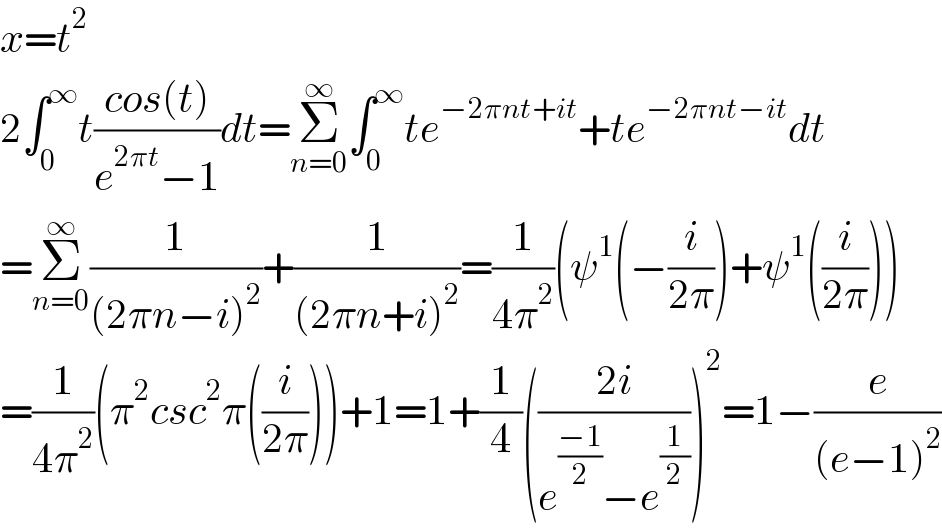
$${x}={t}^{\mathrm{2}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} {t}\frac{{cos}\left({t}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {te}^{−\mathrm{2}\pi{nt}+{it}} +{te}^{−\mathrm{2}\pi{nt}−{it}} {dt} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}−{i}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}+{i}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} }\left(\psi^{\mathrm{1}} \left(−\frac{{i}}{\mathrm{2}\pi}\right)+\psi^{\mathrm{1}} \left(\frac{{i}}{\mathrm{2}\pi}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} }\left(\pi^{\mathrm{2}} {csc}^{\mathrm{2}} \pi\left(\frac{{i}}{\mathrm{2}\pi}\right)\right)+\mathrm{1}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{2}{i}}{{e}^{\frac{−\mathrm{1}}{\mathrm{2}}} −{e}^{\frac{\mathrm{1}}{\mathrm{2}}} }\right)^{\mathrm{2}} =\mathrm{1}−\frac{{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by mnjuly1970 last updated on 27/Feb/21

$${bravo}\:{bravo} \\ $$$${mr}\:{payan}\:…{excellent}… \\ $$
