Question Number 260 by 9999 last updated on 25/Jan/15
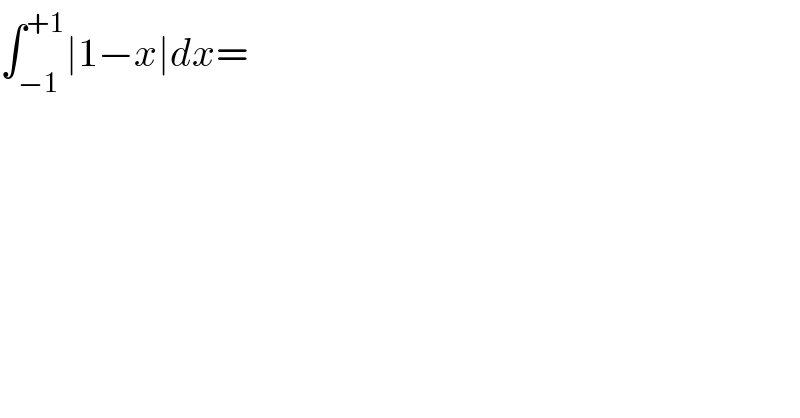
$$\int_{−\mathrm{1}} ^{+\mathrm{1}} \mid\mathrm{1}−{x}\mid{dx}= \\ $$
Answered by 123456 last updated on 17/Dec/14
![∣1−x∣= { ((1−x),(x≤1)),((x−1),(x≥1)) :} ∫_(−1) ^(+1) ∣1−x∣dx=∫_(−1) ^(+1) 1−xdx =[x−(x^2 /2)]_(−1) ^(+1) =[1−(1/2)]−[−1−(1/2)] =1−(1/2)+1+(1/2) =2 ((bh)/2)=((2×2)/2)=2](https://www.tinkutara.com/question/Q263.png)
$$\mid\mathrm{1}−{x}\mid=\begin{cases}{\mathrm{1}−{x}}&{{x}\leqslant\mathrm{1}}\\{{x}−\mathrm{1}}&{{x}\geqslant\mathrm{1}}\end{cases} \\ $$$$\int_{−\mathrm{1}} ^{+\mathrm{1}} \mid\mathrm{1}−{x}\mid{dx}=\int_{−\mathrm{1}} ^{+\mathrm{1}} \mathrm{1}−{xdx} \\ $$$$=\left[{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{−\mathrm{1}} ^{+\mathrm{1}} \\ $$$$=\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right]−\left[−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{2} \\ $$$$\frac{{bh}}{\mathrm{2}}=\frac{\mathrm{2}×\mathrm{2}}{\mathrm{2}}=\mathrm{2} \\ $$
