Question Number 134110 by mohammad17 last updated on 27/Feb/21

Answered by mr W last updated on 27/Feb/21
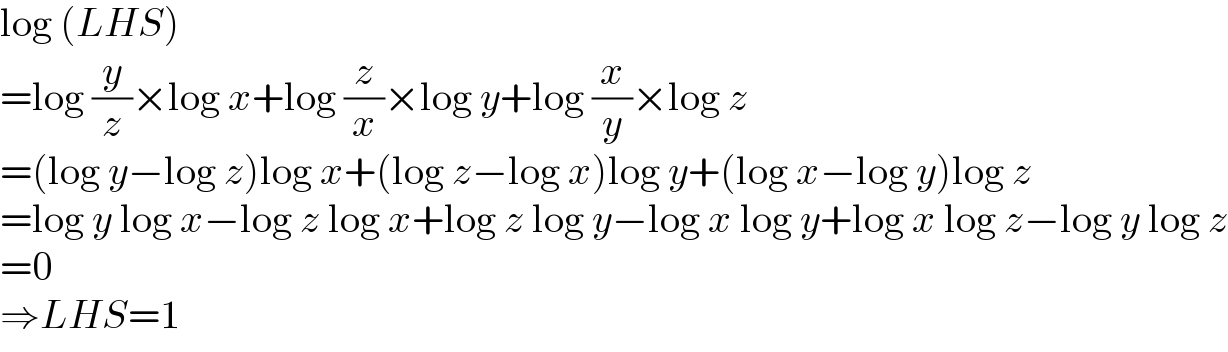
$$\mathrm{log}\:\left({LHS}\right) \\ $$$$=\mathrm{log}\:\frac{{y}}{{z}}×\mathrm{log}\:{x}+\mathrm{log}\:\frac{{z}}{{x}}×\mathrm{log}\:{y}+\mathrm{log}\:\frac{{x}}{{y}}×\mathrm{log}\:{z} \\ $$$$=\left(\mathrm{log}\:{y}−\mathrm{log}\:{z}\right)\mathrm{log}\:{x}+\left(\mathrm{log}\:{z}−\mathrm{log}\:{x}\right)\mathrm{log}\:{y}+\left(\mathrm{log}\:{x}−\mathrm{log}\:{y}\right)\mathrm{log}\:{z} \\ $$$$=\mathrm{log}\:{y}\:\mathrm{log}\:{x}−\mathrm{log}\:{z}\:\mathrm{log}\:{x}+\mathrm{log}\:{z}\:\mathrm{log}\:{y}−\mathrm{log}\:{x}\:\mathrm{log}\:{y}+\mathrm{log}\:{x}\:\mathrm{log}\:{z}−\mathrm{log}\:{y}\:\mathrm{log}\:{z} \\ $$$$=\mathrm{0} \\ $$$$\Rightarrow{LHS}=\mathrm{1} \\ $$
