Question Number 97799 by abdomathmax last updated on 09/Jun/20
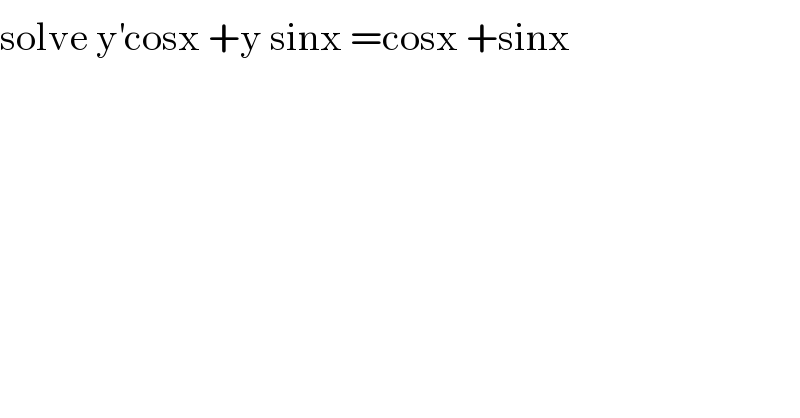
$$\mathrm{solve}\:\mathrm{y}^{'} \mathrm{cosx}\:+\mathrm{y}\:\mathrm{sinx}\:=\mathrm{cosx}\:+\mathrm{sinx} \\ $$
Commented by john santu last updated on 10/Jun/20
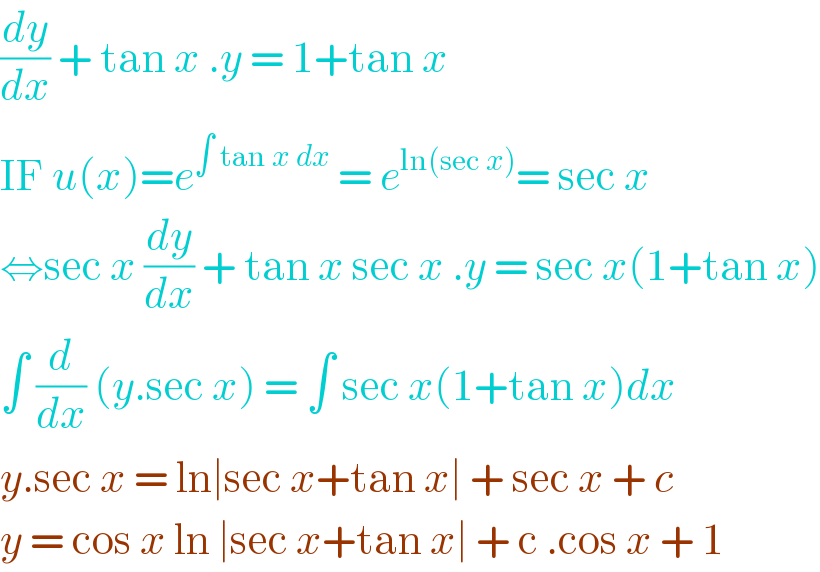
$$\frac{{dy}}{{dx}}\:+\:\mathrm{tan}\:{x}\:.{y}\:=\:\mathrm{1}+\mathrm{tan}\:{x} \\ $$$$\mathrm{IF}\:{u}\left({x}\right)={e}^{\int\:\mathrm{tan}\:{x}\:{dx}} \:=\:{e}^{\mathrm{ln}\left(\mathrm{sec}\:{x}\right)} =\:\mathrm{sec}\:{x} \\ $$$$\Leftrightarrow\mathrm{sec}\:{x}\:\frac{{dy}}{{dx}}\:+\:\mathrm{tan}\:{x}\:\mathrm{sec}\:{x}\:.{y}\:=\:\mathrm{sec}\:{x}\left(\mathrm{1}+\mathrm{tan}\:{x}\right) \\ $$$$\int\:\frac{{d}}{{dx}}\:\left({y}.\mathrm{sec}\:{x}\right)\:=\:\int\:\mathrm{sec}\:{x}\left(\mathrm{1}+\mathrm{tan}\:{x}\right){dx} \\ $$$${y}.\mathrm{sec}\:{x}\:=\:\mathrm{ln}\mid\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\mid\:+\:\mathrm{sec}\:{x}\:+\:{c} \\ $$$${y}\:=\:\mathrm{cos}\:{x}\:\mathrm{ln}\:\mid\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\mid\:+\:\mathrm{c}\:.\mathrm{cos}\:{x}\:+\:\mathrm{1}\: \\ $$
