Menu Close

dx-cosx-sin-3-x-sinx-cos-3-x-

Tinku Tara 0 Comments
Pin




Question Number 163414 by AbdullahIbrahim last updated on 06/Jan/22
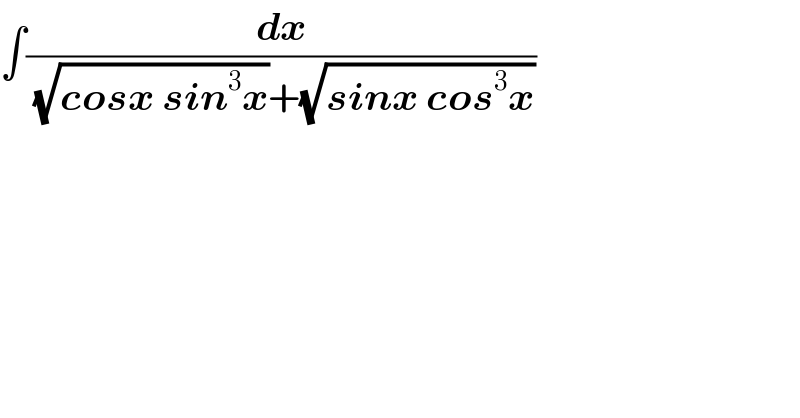
∫(dx/( (√(cosx sin^3 x))+(√(sinx cos^3 x))))
$$\int\frac{\boldsymbol{{dx}}}{\:\sqrt{\boldsymbol{{cosx}}\:\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{x}}}+\sqrt{\boldsymbol{{sinx}}\:\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{x}}}} \\ $$
Answered by Ar Brandon last updated on 06/Jan/22
I=∫(dx/( (√(cosxsin^3 x))+(√(sinxcos^3 x)))) =∫(((√(sinxcos^3 x))−(√(cosxsin^3 x)))/(sinxcos^3 x−cosxsin^3 x))dx =∫((cosx(√(sinxcosx)))/(sinxcosxcos2x))dx−∫((sinx(√(sinxcosx)))/(sinxcosxcos2x))dx =∫((√(cotx))/(cos2x))dx−∫((√(tanx))/(cos2x))dx =∫((cosec^2 x)/( cot^2 x−1))(√(cotx))dx−∫((sec^2 x)/(1−tan^2 x))(√(tanx))dx =∫((√u)/(1−u^2 ))du−∫((√v)/(1−v^2 ))dv=∫((2p^2 )/(1−p^4 ))dp−∫((2q^2 )/(1−q^4 ))dq =∫(((q^2 +1)+(q^2 −1))/(q^4 −1))dq−∫(((p^2 +1)+(p^2 −1))/(p^4 −1))dp =∫((1/(q^2 −1))+(1/(q^2 +1)))dq−∫((1/(p^2 −1))+(1/(p^2 +1)))dp =arctan(q)−(1/2)ln∣((1+q)/(1−q))∣+(1/2)ln∣((1+p)/(1−p))∣−arctan(p)+C =arctan((√(tanx)))−(1/2)ln∣((1+(√(tanx)))/(1−(√(tanx))))∣+ (1/2)ln∣((1+(√(cotx)))/(1−(√(cotx))))∣−arctan((√(cotx)))+C
$${I}=\int\frac{{dx}}{\:\sqrt{\mathrm{cos}{x}\mathrm{sin}^{\mathrm{3}} {x}}+\sqrt{\mathrm{sin}{x}\mathrm{cos}^{\mathrm{3}} {x}}} \\ $$$$\:\:\:=\int\frac{\sqrt{\mathrm{sin}{x}\mathrm{cos}^{\mathrm{3}} {x}}−\sqrt{\mathrm{cos}{x}\mathrm{sin}^{\mathrm{3}} {x}}}{\mathrm{sin}{x}\mathrm{cos}^{\mathrm{3}} {x}−\mathrm{cos}{x}\mathrm{sin}^{\mathrm{3}} {x}}{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{cos}{x}\sqrt{\mathrm{sin}{x}\mathrm{cos}{x}}}{\mathrm{sin}{x}\mathrm{cos}{x}\mathrm{cos2}{x}}{dx}−\int\frac{\mathrm{sin}{x}\sqrt{\mathrm{sin}{x}\mathrm{cos}{x}}}{\mathrm{sin}{x}\mathrm{cos}{x}\mathrm{cos2}{x}}{dx} \\ $$$$\:\:\:=\int\frac{\sqrt{\mathrm{cot}{x}}}{\mathrm{cos2}{x}}{dx}−\int\frac{\sqrt{\mathrm{tan}{x}}}{\mathrm{cos2}{x}}{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{cosec}^{\mathrm{2}} {x}}{\:\mathrm{cot}^{\mathrm{2}} {x}−\mathrm{1}}\sqrt{\mathrm{cot}{x}}{dx}−\int\frac{\mathrm{sec}^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {x}}\sqrt{\mathrm{tan}{x}}{dx} \\ $$$$\:\:\:=\int\frac{\sqrt{{u}}}{\mathrm{1}−{u}^{\mathrm{2}} }{du}−\int\frac{\sqrt{{v}}}{\mathrm{1}−{v}^{\mathrm{2}} }{dv}=\int\frac{\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{1}−{p}^{\mathrm{4}} }{dp}−\int\frac{\mathrm{2}{q}^{\mathrm{2}} }{\mathrm{1}−{q}^{\mathrm{4}} }{dq} \\ $$$$\:\:\:=\int\frac{\left({q}^{\mathrm{2}} +\mathrm{1}\right)+\left({q}^{\mathrm{2}} −\mathrm{1}\right)}{{q}^{\mathrm{4}} −\mathrm{1}}{dq}−\int\frac{\left({p}^{\mathrm{2}} +\mathrm{1}\right)+\left({p}^{\mathrm{2}} −\mathrm{1}\right)}{{p}^{\mathrm{4}} −\mathrm{1}}{dp} \\ $$$$\:\:\:=\int\left(\frac{\mathrm{1}}{{q}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{{q}^{\mathrm{2}} +\mathrm{1}}\right){dq}−\int\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}\right){dp} \\ $$$$\:\:\:=\mathrm{arctan}\left({q}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+{q}}{\mathrm{1}−{q}}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+{p}}{\mathrm{1}−{p}}\mid−\mathrm{arctan}\left({p}\right)+{C} \\ $$$$\:\:\:=\mathrm{arctan}\left(\sqrt{\mathrm{tan}{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{tan}{x}}}{\mathrm{1}−\sqrt{\mathrm{tan}{x}}}\mid+ \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{cot}{x}}}{\mathrm{1}−\sqrt{\mathrm{cot}{x}}}\mid−\mathrm{arctan}\left(\sqrt{\mathrm{cot}{x}}\right)+{C} \\ $$
Commented by peter frank last updated on 07/Jan/22
great
$$\mathrm{great} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *