Menu Close

let-F-x-0-pi-ln-1-xcos-d-with-x-lt-1-find-F-x-

Tinku Tara 0 Comments
Pin




Question Number 32365 by prof Abdo imad last updated on 23/Mar/18
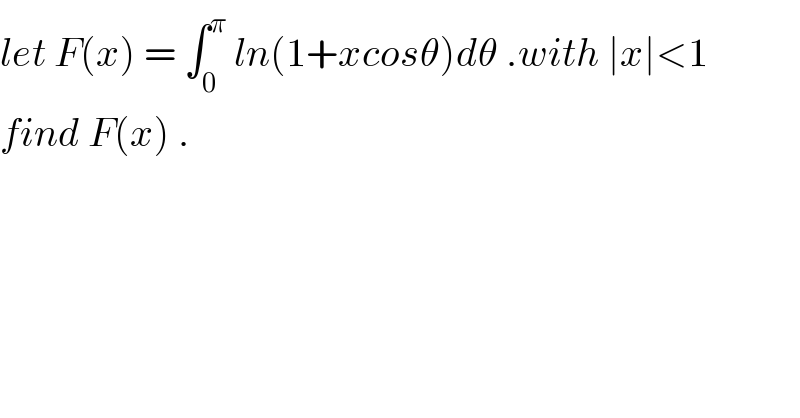
let F(x) = ∫_0 ^π ln(1+xcosθ)dθ .with ∣x∣<1 find F(x) .
$${let}\:{F}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{xcos}\theta\right){d}\theta\:.{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${find}\:{F}\left({x}\right)\:. \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18
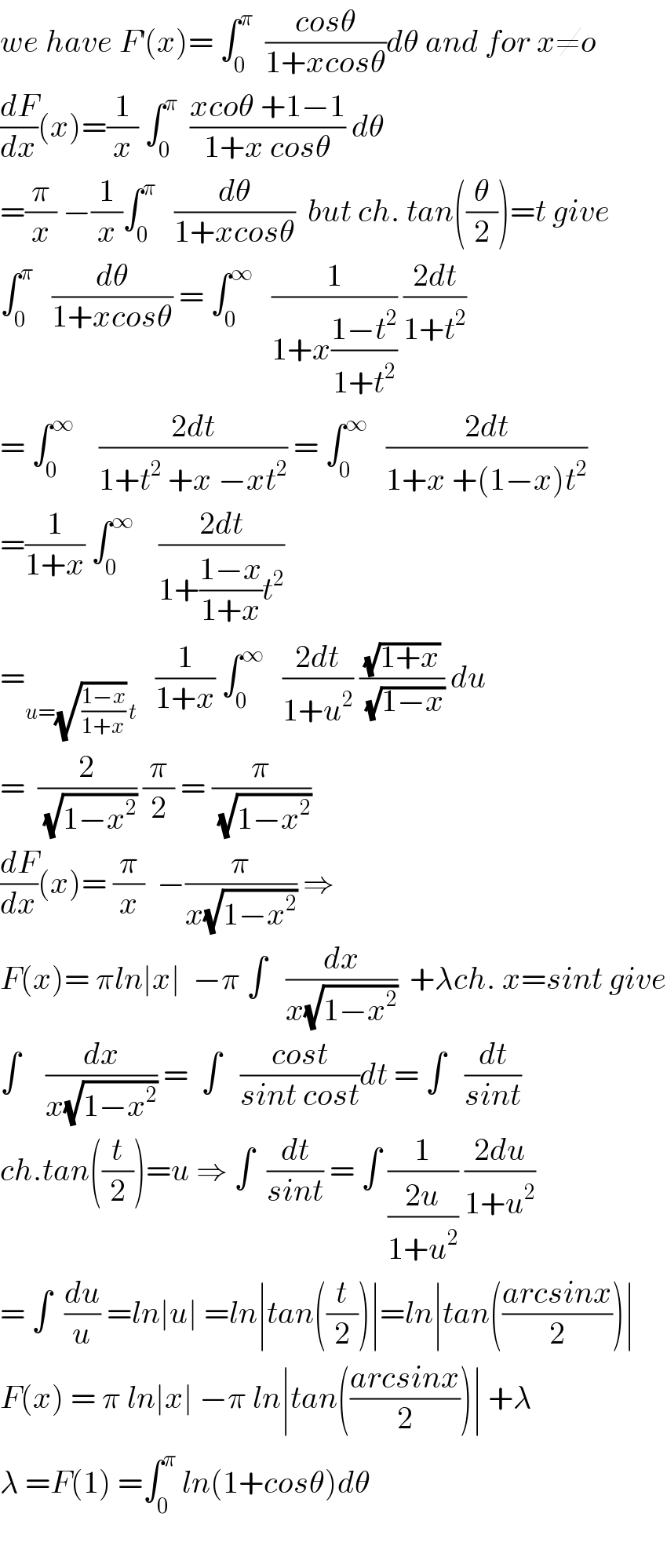
we have F^′ (x)= ∫_0 ^π ((cosθ)/(1+xcosθ))dθ and for x≠o (dF/dx)(x)=(1/x) ∫_0 ^π ((xcoθ +1−1)/(1+x cosθ)) dθ =(π/x) −(1/x)∫_0 ^π (dθ/(1+xcosθ)) but ch. tan((θ/2))=t give ∫_0 ^π (dθ/(1+xcosθ)) = ∫_0 ^∞ (1/(1+x((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^∞ ((2dt)/(1+t^2 +x −xt^2 )) = ∫_0 ^∞ ((2dt)/(1+x +(1−x)t^2 )) =(1/(1+x)) ∫_0 ^∞ ((2dt)/(1+((1−x)/(1+x))t^2 )) =_(u=(√((1−x)/(1+x))) t) (1/(1+x)) ∫_0 ^∞ ((2dt)/(1+u^2 )) ((√(1+x))/( (√(1−x)))) du = (2/( (√(1−x^2 )))) (π/2) = (π/( (√(1−x^2 )))) (dF/dx)(x)= (π/x) −(π/(x(√(1−x^2 )))) ⇒ F(x)= πln∣x∣ −π ∫ (dx/(x(√(1−x^2 )))) +λch. x=sint give ∫ (dx/(x(√(1−x^2 )))) = ∫ ((cost)/(sint cost))dt = ∫ (dt/(sint)) ch.tan((t/2))=u ⇒ ∫ (dt/(sint)) = ∫ (1/((2u)/(1+u^2 ))) ((2du)/(1+u^2 )) = ∫ (du/u) =ln∣u∣ =ln∣tan((t/2))∣=ln∣tan(((arcsinx)/2))∣ F(x) = π ln∣x∣ −π ln∣tan(((arcsinx)/2))∣ +λ λ =F(1) =∫_0 ^π ln(1+cosθ)dθ
$${we}\:{have}\:{F}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{cos}\theta}{\mathrm{1}+{xcos}\theta}{d}\theta\:{and}\:{for}\:{x}\neq{o} \\ $$$$\frac{{dF}}{{dx}}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{xco}\theta\:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{x}\:{cos}\theta}\:{d}\theta \\ $$$$=\frac{\pi}{{x}}\:−\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\mathrm{1}+{xcos}\theta}\:\:{but}\:{ch}.\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\mathrm{1}+{xcos}\theta}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+{x}\:−{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{x}\:+\left(\mathrm{1}−{x}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}{t}^{\mathrm{2}} } \\ $$$$=_{{u}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:{t}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{\mathrm{1}−{x}}}\:{du} \\ $$$$=\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\frac{\pi}{\mathrm{2}}\:=\:\frac{\pi}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\frac{{dF}}{{dx}}\left({x}\right)=\:\frac{\pi}{{x}}\:\:−\frac{\pi}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\pi{ln}\mid{x}\mid\:\:−\pi\:\int\:\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:+\lambda{ch}.\:{x}={sint}\:{give} \\ $$$$\int\:\:\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\:\:\int\:\:\:\frac{{cost}}{{sint}\:{cost}}{dt}\:=\:\int\:\:\:\frac{{dt}}{{sint}} \\ $$$${ch}.{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:\Rightarrow\:\int\:\:\frac{{dt}}{{sint}}\:=\:\int\:\frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\frac{{du}}{{u}}\:={ln}\mid{u}\mid\:={ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}\right)\mid={ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid \\ $$$${F}\left({x}\right)\:=\:\pi\:{ln}\mid{x}\mid\:−\pi\:{ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid\:+\lambda \\ $$$$\lambda\:={F}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{cos}\theta\right){d}\theta \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18
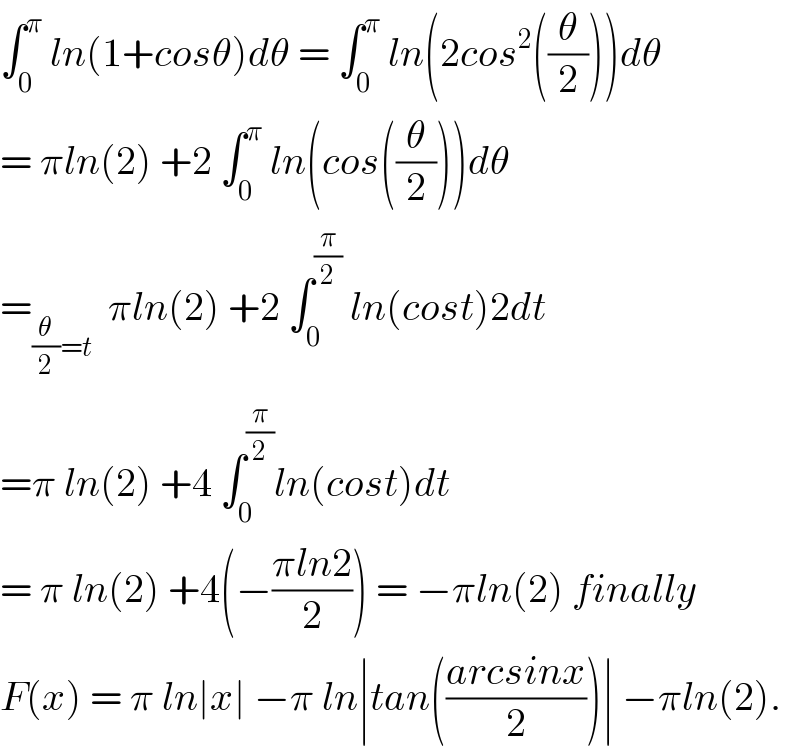
∫_0 ^π ln(1+cosθ)dθ = ∫_0 ^π ln(2cos^2 ((θ/2)))dθ = πln(2) +2 ∫_0 ^π ln(cos((θ/2)))dθ =_((θ/2)=t) πln(2) +2 ∫_0 ^(π/2) ln(cost)2dt =π ln(2) +4 ∫_0 ^(π/2) ln(cost)dt = π ln(2) +4(−((πln2)/2)) = −πln(2) finally F(x) = π ln∣x∣ −π ln∣tan(((arcsinx)/2))∣ −πln(2).
$$\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{cos}\theta\right){d}\theta\:=\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$=\:\pi{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left({cos}\left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$=_{\frac{\theta}{\mathrm{2}}={t}} \:\:\pi{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cost}\right)\mathrm{2}{dt} \\ $$$$=\pi\:{ln}\left(\mathrm{2}\right)\:+\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cost}\right){dt} \\ $$$$=\:\pi\:{ln}\left(\mathrm{2}\right)\:+\mathrm{4}\left(−\frac{\pi{ln}\mathrm{2}}{\mathrm{2}}\right)\:=\:−\pi{ln}\left(\mathrm{2}\right)\:{finally} \\ $$$${F}\left({x}\right)\:=\:\pi\:{ln}\mid{x}\mid\:−\pi\:{ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid\:−\pi{ln}\left(\mathrm{2}\right). \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18
F(0) =0
$${F}\left(\mathrm{0}\right)\:=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *