Menu Close

Question-131334

Tinku Tara
Pin




Question Number 131334 by Algoritm last updated on 03/Feb/21
Answered by bluberry508 last updated on 06/Feb/21
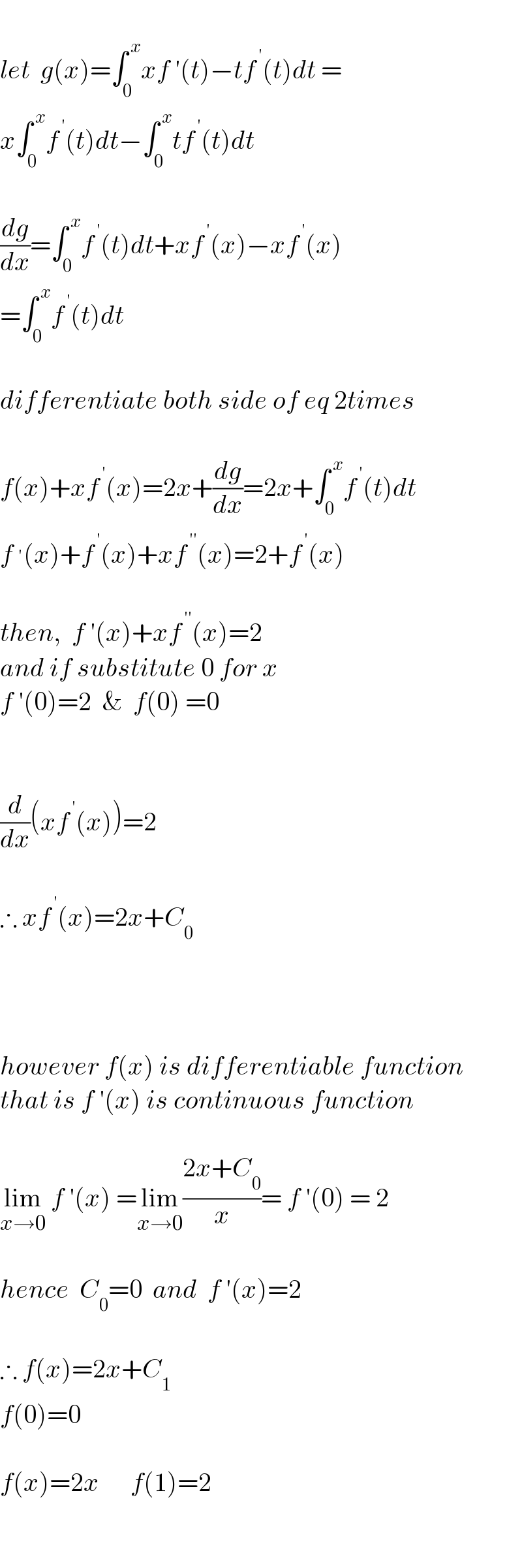
let g(x)=∫_0 ^( x) xf ′(t)−tf^( ′) (t)dt = x∫_0 ^( x) f^( ′) (t)dt−∫_0 ^( x) tf^( ′) (t)dt (dg/dx)=∫_0 ^( x) f^( ′) (t)dt+xf^( ′) (x)−xf^( ′) (x) =∫_0 ^( x) f^( ′) (t)dt differentiate both side of eq 2times f(x)+xf^( ′) (x)=2x+(dg/dx)=2x+∫_0 ^( x) f^( ′) (t)dt f^′ (x)+f^( ′) (x)+xf^( ′′) (x)=2+f^( ′) (x) then, f ′(x)+xf^( ′′) (x)=2 and if substitute 0 for x f ′(0)=2 & f(0) =0 (d/dx)(xf^( ′) (x))=2 ∴ xf^( ′) (x)=2x+C_0 however f(x) is differentiable function that is f ′(x) is continuous function lim_(x→0) f ′(x) =lim_(x→0) ((2x+C_0 )/x)= f ′(0) = 2 hence C_0 =0 and f ′(x)=2 ∴ f(x)=2x+C_1 f(0)=0 f(x)=2x f(1)=2
$$ \\ $$$${let}\:\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} {xf}\:'\left({t}\right)−{tf}^{\:'} \left({t}\right){dt}\:= \\ $$$${x}\int_{\mathrm{0}} ^{\:{x}} {f}^{\:'} \left({t}\right){dt}−\int_{\mathrm{0}} ^{\:{x}} {tf}^{\:'} \left({t}\right){dt} \\ $$$$ \\ $$$$\frac{{dg}}{{dx}}=\int_{\mathrm{0}} ^{\:{x}} {f}^{\:'} \left({t}\right){dt}+{xf}^{\:'} \left({x}\right)−{xf}^{\:'} \left({x}\right) \\ $$$$=\int_{\mathrm{0}} ^{\:{x}} {f}^{\:'} \left({t}\right){dt} \\ $$$$ \\ $$$${differentiate}\:{both}\:{side}\:{of}\:{eq}\:\mathrm{2}{times} \\ $$$$ \\ $$$${f}\left({x}\right)+{xf}^{\:'} \left({x}\right)=\mathrm{2}{x}+\frac{{dg}}{{dx}}=\mathrm{2}{x}+\int_{\mathrm{0}} ^{\:{x}} {f}^{\:'} \left({t}\right){dt} \\ $$$${f}\:^{'} \left({x}\right)+{f}^{\:'} \left({x}\right)+{xf}^{\:''} \left({x}\right)=\mathrm{2}+{f}^{\:'} \left({x}\right) \\ $$$$ \\ $$$${then},\:\:{f}\:'\left({x}\right)+{xf}^{\:''} \left({x}\right)=\mathrm{2} \\ $$$${and}\:{if}\:{substitute}\:\mathrm{0}\:{for}\:{x}\: \\ $$$${f}\:'\left(\mathrm{0}\right)=\mathrm{2}\:\:\&\:\:{f}\left(\mathrm{0}\right)\:=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$\frac{{d}}{{dx}}\left({xf}^{\:'} \left({x}\right)\right)=\mathrm{2} \\ $$$$ \\ $$$$\therefore\:{xf}^{\:'} \left({x}\right)=\mathrm{2}{x}+{C}_{\mathrm{0}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${however}\:{f}\left({x}\right)\:{is}\:{differentiable}\:{function} \\ $$$${that}\:{is}\:{f}\:'\left({x}\right)\:{is}\:{continuous}\:{function} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\:'\left({x}\right)\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{x}+{C}_{\mathrm{0}} }{{x}}=\:{f}\:'\left(\mathrm{0}\right)\:=\:\mathrm{2} \\ $$$$ \\ $$$${hence}\:\:{C}_{\mathrm{0}} =\mathrm{0}\:\:{and}\:\:{f}\:'\left({x}\right)=\mathrm{2} \\ $$$$ \\ $$$$\therefore\:{f}\left({x}\right)=\mathrm{2}{x}+{C}_{\mathrm{1}} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$ \\ $$$${f}\left({x}\right)=\mathrm{2}{x}\:\:\:\:\:\:{f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$

Pin