Question Number 97972 by Aniruddha Ghosh last updated on 10/Jun/20
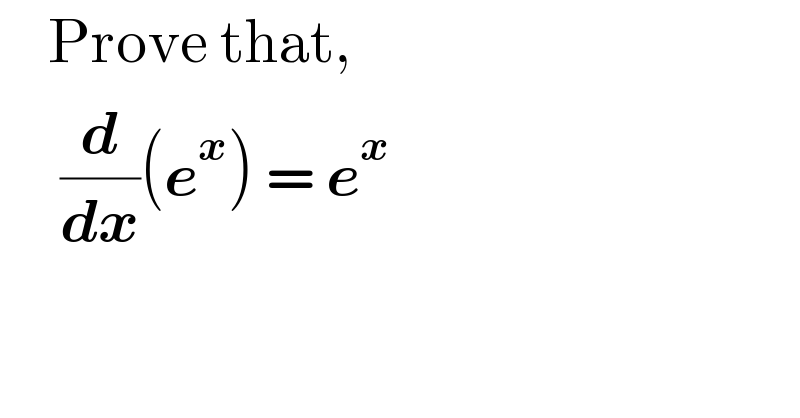
$$\:\:\:\:\mathrm{Prove}\:\mathrm{that}, \\ $$$$\:\:\:\:\:\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} \right)\:=\:\boldsymbol{{e}}^{\boldsymbol{{x}}} \\ $$
Answered by abdomathmax last updated on 10/Jun/20
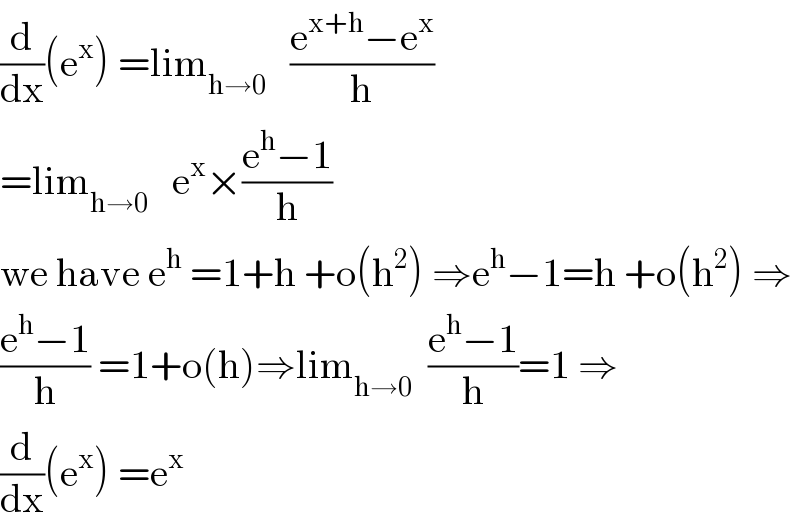
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{e}^{\mathrm{x}} \right)\:=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{e}^{\mathrm{x}+\mathrm{h}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{h}} \\ $$$$=\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\:\mathrm{e}^{\mathrm{x}} ×\frac{\mathrm{e}^{\mathrm{h}} −\mathrm{1}}{\mathrm{h}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{e}^{\mathrm{h}} \:=\mathrm{1}+\mathrm{h}\:+\mathrm{o}\left(\mathrm{h}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{e}^{\mathrm{h}} −\mathrm{1}=\mathrm{h}\:+\mathrm{o}\left(\mathrm{h}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\frac{\mathrm{e}^{\mathrm{h}} −\mathrm{1}}{\mathrm{h}}\:=\mathrm{1}+\mathrm{o}\left(\mathrm{h}\right)\Rightarrow\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{e}^{\mathrm{h}} −\mathrm{1}}{\mathrm{h}}=\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{e}^{\mathrm{x}} \right)\:=\mathrm{e}^{\mathrm{x}} \\ $$
Answered by MJS last updated on 10/Jun/20
![(d/dx)[f(x)]=lim_(h→0) ((f(x+h)−f(x−h))/(2h)) (d/dx)[e^x ]=lim_(h→0) ((e^(x+h) −e^(x−h) )/(2h)) =lim_(h→0) ((e^h −e^(−h) )/(2h))e^x = =e^x ×lim_(h→0) ((sinh h)/h) = [l′Hopital] =e^x ×lim_(h→0) (((d/dh)[sinh h])/((d/dh)[h]))=e^x ×lim_(h→0) cosh h =e^x](https://www.tinkutara.com/question/Q97976.png)
$$\frac{{d}}{{dx}}\left[{f}\left({x}\right)\right]=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}+{h}\right)−{f}\left({x}−{h}\right)}{\mathrm{2}{h}} \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{e}^{{x}} \right]=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{{x}+{h}} −\mathrm{e}^{{x}−{h}} }{\mathrm{2}{h}}\:=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{{h}} −\mathrm{e}^{−{h}} }{\mathrm{2}{h}}\mathrm{e}^{{x}} \:= \\ $$$$=\mathrm{e}^{{x}} ×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sinh}\:{h}}{{h}}\:= \\ $$$$\:\:\:\:\:\left[\mathrm{l}'\mathrm{Hopital}\right] \\ $$$$=\mathrm{e}^{{x}} ×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}}{{dh}}\left[\mathrm{sinh}\:{h}\right]}{\frac{{d}}{{dh}}\left[{h}\right]}=\mathrm{e}^{{x}} ×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{cosh}\:{h}\:=\mathrm{e}^{{x}} \\ $$
Answered by smridha last updated on 10/Jun/20
![(i)(d/dx)(e^x )=lim_(h→0) ((e^(x+h) −e^x )/h)[just using the definetion] [that (df/dx)=lim_(h→0) ((f(x+h)−f(x))/h)] so we get: =e^x [lim_(h→0) ((e^h −1)/h)]=e^x .1=e^x . (ii)now do it by series expanssion e^x =Σ_(n=0) ^∞ (x^n /(n!))=1+(x/(1!))+(x^2 /(2!))+(x^3 /(3!))+.....+(x^n /(n!))+(x^(n+1) /((n+1)!))+....∞ now diff:wrt x we get (d/dx)(e^x )=0+[1+(x/(1!))+(x^2 /(2!))+(x^3 /(3!))+...+(x^(n−1) /((n−1)!))+(x^n /(n!))+...∞] =0+e^x =e^x [its remain the as it is]](https://www.tinkutara.com/question/Q97980.png)
$$\left(\boldsymbol{{i}}\right)\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} \right)=\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{h}}} −\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\boldsymbol{{h}}}\left[\boldsymbol{{just}}\:\boldsymbol{{using}}\:\boldsymbol{{the}}\:\boldsymbol{{definetion}}\right] \\ $$$$\left[\boldsymbol{{that}}\:\frac{\boldsymbol{{df}}}{\boldsymbol{{dx}}}=\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{f}}\left(\boldsymbol{{x}}+\boldsymbol{{h}}\right)−\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{h}}}\right] \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{we}}\:\boldsymbol{{get}}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{e}}^{\boldsymbol{{x}}} \left[\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{e}}^{\boldsymbol{{h}}} −\mathrm{1}}{\boldsymbol{{h}}}\right]=\boldsymbol{{e}}^{\boldsymbol{{x}}} .\mathrm{1}=\boldsymbol{{e}}^{\boldsymbol{{x}}} . \\ $$$$\left(\boldsymbol{{ii}}\right)\boldsymbol{{now}}\:\boldsymbol{{do}}\:\boldsymbol{{it}}\:\boldsymbol{{by}}\:\boldsymbol{{series}}\:\boldsymbol{{expanssion}} \\ $$$$\:\boldsymbol{{e}}^{\boldsymbol{{x}}} =\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\boldsymbol{{x}}^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!}=\mathrm{1}+\frac{\boldsymbol{{x}}}{\mathrm{1}!}+\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}!}+…..+\frac{\boldsymbol{{x}}^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!}+\frac{\boldsymbol{{x}}^{\boldsymbol{{n}}+\mathrm{1}} }{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}+….\infty \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{diff}}:\boldsymbol{{wrt}}\:\boldsymbol{{x}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} \right)=\mathrm{0}+\left[\mathrm{1}+\frac{\boldsymbol{{x}}}{\mathrm{1}!}+\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}!}+…+\frac{{x}^{\boldsymbol{{n}}−\mathrm{1}} }{\left(\boldsymbol{{n}}−\mathrm{1}\right)!}+\frac{\boldsymbol{{x}}^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!}+…\infty\right] \\ $$$$\:\:\:\:\:=\mathrm{0}+\boldsymbol{{e}}^{\boldsymbol{{x}}} =\boldsymbol{{e}}^{\boldsymbol{{x}}} \left[\boldsymbol{{its}}\:\boldsymbol{{remain}}\:\boldsymbol{{the}}\:\boldsymbol{{as}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\right] \\ $$
Commented by MathGod last updated on 10/Jun/20

$$\mathbb{I}\:\mathbb{USE}\:\mathbb{THE}\:\mathbb{REDDEST}\:\mathbb{INK}! \\ $$
Commented by arcana last updated on 11/Jun/20

$$\mathrm{using}\:{e}^{{h}} −\mathrm{1}−{h}\geqslant\mathrm{0},\:\forall{h}\in\mathbb{R} \\ $$$$\mathrm{then}\:\mathrm{1}\leqslant\frac{{e}^{{h}} −\mathrm{1}}{{h}}\leqslant\mathrm{1} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{e}^{{h}} −\mathrm{1}}{{h}}=\mathrm{1}\: \\ $$$$ \\ $$
